初中数学浙教版七年级下学期期中复习专题8 平方差公式的运用和几何背景

试卷更新日期：2021-04-07 类型：复习试卷

进入出卷网下载

一、单选题

1. $(1 + y) (1 - y) =$ （）

A、 $1 + y^{2}$ B、 $- 1 - y^{2}$ C、 $1 - y^{2}$ D、 $- 1 + y^{2}$

查看试题解析
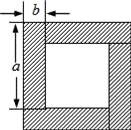
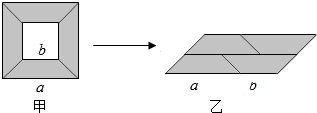
2. 下列各式中，能用平方差公式计算的是（）

A、(-a-b)(a+b) B、(-a-b)(a-b) C、(-a+b-c)(-a+b-c) D、(-a+b)(a-b)

查看试题解析
3. 下列运算正确的是（）

A、（m﹣n）（﹣m﹣n）＝﹣m²﹣n² B、（﹣1+mn）（1+mn）＝﹣1﹣m²n² C、（﹣m+n）（m﹣n）＝m²﹣n² D、（2m﹣3）（2m+3）＝4m²﹣9

查看试题解析
4. 如果x+y＝6，x²-y²=24，那么y-x的值为（）

A、﹣4 B、4 C、﹣6 D、6

查看试题解析
5. 若|x+y﹣5|+（x﹣y﹣3）²=0，则x²﹣y²的结果是（）

A、2 B、8 C、15 D、16

查看试题解析
6. 如图，从边长为 $a$ 的大正方形纸片中挖去一个边长为 $b$ 的小正方形纸片后，将其裁成四个相同的等腰梯形（甲），然后拼成一个平行四边形（乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式是（）

A、 ${(a - b)}^{2} = a^{2} - b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
7. 若 $a^{2} - 4 b^{2} = 12$ ， $a - 2 b = 2$ ，则 $a^{b}$ 的值为（）

A、4 B、-4 C、 $- \frac{1}{4}$ D、 $\frac{1}{4}$

查看试题解析
8. (a^m-bⁿ)(a^m+bⁿ)等于（）

A、a^2m-b²ⁿ B、am²-bm² C、a^2m+b²ⁿ D、b²ⁿ-a^2m

查看试题解析
9. （x＋2）（x－2）（x²＋4）的计算结果是（）

A、x⁴＋16 B、－x⁴－16 C、x⁴－16 D、16－x⁴

查看试题解析
10. 用简便方法计算，将99×101变形正确的是（）

A、 $99 \times 101 = 100^{2} + 1^{2}$ B、 $99 \times 101 = {(100 - 1)}^{2}$ C、 $99 \times 101 = 100^{2} - 1^{2}$ D、 $99 \times 101 = {(100 + 1)}^{2}$

查看试题解析

二、填空题

11. 分解因式： $m^{2} - 25 =$ .

查看试题解析
12. 已知 $m + n = 12$ ， $m - n = 2$ ，则 $m^{2} - n^{2} =$ .

查看试题解析
13. 若 $a$ ， $b$ 互为相反数，则 $a^{2} - b^{2} =$ .

查看试题解析
14. 计算： $58 \times 62 =$ .

查看试题解析
15. 如果（2a＋2b＋1）（2a＋2b－1）＝63，那么a＋b的值为．

查看试题解析
16. 计算：（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）=（结果可用幂的形式表示）

查看试题解析

三、解答题

17. 计算： $10 \frac{1}{7} \times 9 \frac{6}{7}$

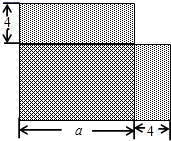
查看试题解析
18. 利用乘法公式计算： $2020^{2} - 2019 \times 2021$

查看试题解析
19. 已知： $a^{2} + b^{2} = 5$ ， ${(3 a - 2 b)}^{2} - {(3 a + 2 b)}^{2} = - 48$ ，求 $a + b$ 的值．

查看试题解析
20. 如图，有一位狡猾的地主，把一块边长为a的正方形的土地，租给李老汉种植，他对李老汉说：“我把你这块地的一边减少4m，另一边增加4m，继续租给你，你也没有吃亏，你看如何”.李老汉一听，觉得自己好像没有吃亏，就答应了.同学们，你们觉得李老汉有没有吃亏？请说明理由.

查看试题解析
21. 老师在黑板上写了三个算式，希望同学们认真观察，发现规律.请你结合这些算式，解答下列问题：
请观察以下算式：

① $3^{2} - 1^{2} = 8 \times 1$ ；

② $5^{2} - 3^{2} = 8 \times 2$ ；

③ $7^{2} - 5^{2} = 8 \times 3$ ；

……

试写出符合上述规律的第五个算式；

验证：设两个连续奇数为2n+1， $2 n - 1$ (其中 $n$ 为正整数)，并说明它们的平方差是8的倍数；

查看试题解析
22. 试判断 $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots \dots (1 - \frac{1}{n^{2}})$ 的值与 $\frac{1}{2}$ 的大小关系，并证明你的结论.

查看试题解析
23. 用四块完全相同的小长方形拼成的一个“回形”正方形．

(1)、用不同代数式表示图中的阴影部分的面积，你能得到怎样的等式，试用乘法公式说明这个等式成立；

(2)、利用（1）中的结论计算： $a + b = 2$ ， $a b = \frac{3}{4}$ ，求 $a - b$ ；

(3)、根据（1）中的结论，直接写出 $x + \frac{1}{x}$ 和 $x - \frac{1}{x}$ 之间的关系；若 $x^{2} - 3 x + 1 = 0$ ，分别求出 $x + \frac{1}{x}$ 和 ${(x - \frac{1}{x})}^{2}$ 的值．

查看试题解析
24. 王华由 $5^{2} - 3^{2} = 8 \times 2$ ， $9^{2} - 7^{2} = 8 \times 4$ ， $15^{2} - 3^{2} = 8 \times 27$ ， $11^{2} - 5^{2} = 8 \times 12$ ， $15^{2} - 7^{2} = 8 \times 22$ ，这些算式发现：任意两个奇数的平方差都是8的倍数

(1)、请你再写出两个（不同于上面算式）具有上述规律的算式；

(2)、请你用含字母的代数式概括王华发现的这个规律（提示：可以使用多个字母）；

(3)、证明这个规律的符合题意性.

查看试题解析