初中数学浙教版七年级下学期期中复习专题6 三元一次方程组

试卷更新日期：2021-04-07 类型：复习试卷

进入出卷网下载

一、单选题

1. 解三元一次方程组 ${\begin{cases} x - y + z = - 3 ， ① \\ x + 2 y - z = 1 ， ② \\ x + y = 0 ， ③ \end{cases}$ 要使解法较为简便，首先应进行的变形为（）

A、①+② B、①-② C、①+③ D、②-③

查看试题解析
2. 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）

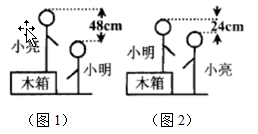A、① B、② C、③ D、④

查看试题解析
3. 三元一次方程组 ${\begin{array}{l} x + y = 3 \\ y + z = 5 \\ x + z = 4 \end{array}$ ，的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 3 \\ z = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2 \\ z = 3 \end{array}$

查看试题解析
4. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，有多少种购买方案（）

A、12种 B、15种 C、16种 D、14种

查看试题解析
5. 下列方程组中，是三元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ y + z = 1 \\ z + w = 5 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ y + 2 x = 1 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 z = 7 \\ 2 x + 3 y = 9 - z \\ 5 x - 9 y + 7 z = 8 \end{array}$ D、 ${\begin{array}{l} x^{2} - 2 y = 0 \\ y + z = 3 \\ x + y + z = 1 \end{array}$

查看试题解析
6. 三元一次方程组 ${\begin{array}{l} 2 x = 3 y = 6 z \\ x + 2 y + z = 16 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 3 \\ z = 5 \end{array}$ B、 ${\begin{array}{l} x = 6 \\ y = 3 \\ z = 2 \end{array}$ C、 ${\begin{array}{l} x = 6 \\ y = 4 \\ z = 2 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 5 \\ z = 6 \end{array}$

查看试题解析
7. 已知方程组 ${\begin{array}{l} x + y = 3 \\ y + z = - 2 \\ z + x = 9 \end{array}$ ，则x＋y＋z的值为（）

A、6 B、－6 C、5 D、－5

查看试题解析
8. 利用两块长方体木块测量两张桌子的高度.首先按图 $①$ 方式放置，再交换两木块的位置，按图 $②$ 方式放置.测量的数据如图，则桌子高度是（）

A、 $74 c m$ B、 $75 c m$ C、 $76 c m$ D、 $77 c m$

查看试题解析
9. 一宾馆有二人间、三人间、四人间三种客房供游客居住，某旅行团24人准备同时订这三种客房共8间，且每个客房都住满，那么订房方案有（）

A、4种 B、3种 C、2种 D、1种

查看试题解析
10. 对于三元一次方程组，我们一般是先消去一个未知数，转化为二元一次方程组求解。那么在解三元一次方程组 ${\begin{matrix} 2 x + y + z = 9 \\ x + 2 y + z = 8 \\ x + y + 2 z = 7 \end{matrix}$ 时，下列没有实现这一转化的是（）

A、 ${\begin{matrix} x - y = 1 \\ y - z = 1 \end{matrix}$ B、 ${\begin{matrix} x - y = 1 \\ 3 x + y = 11 \end{matrix}$ C、 ${\begin{matrix} x - z = 2 \\ 3 x + z = 10 \end{matrix}$ D、 ${\begin{matrix} y - z = 1 \\ 3 y + z = 7 \end{matrix}$

查看试题解析

二、填空题

11. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析
12. 有A、B、C三种商品，如果购5件A、2件B、3件C共需513元，购3件A、6件B、5件C共需375件，那么购A、B、C各一件共需元.

查看试题解析
13. 为防控新冠疫情，做好个人防护，小君去药店购买口罩，若买6个平面口罩和4个 $K N 95$ 口罩，则她所带的钱还剩下10元；若买4个平面口罩和6个 $K N 95$ 口罩，则她所带的钱还缺8元，若只买10个 $K N 95$ 口罩，则她所带的钱还缺元.

查看试题解析
14. 为确保信息安全，在传输时往往需加密，发送方发出一组密码a，b，c时，则接收方对应收到的密码为A，B，C，双方约定：A＝2a－b，B＝2b，C＝b＋c，例如发出的密码是1，2，3，则收到的密码是0，4，5.若接收方收到的密码是2，8，11时，则发送方发出的密码是

查看试题解析
15. 有甲、乙、丙三种商品，如果购甲3件、乙2件，丙1件共需315元钱，购甲2件、乙3件、丙4件共需285元钱，那么购甲、乙、丙三种商品各一件共需元钱．

查看试题解析
16. 若x＋y＋z＝15，－3x－y＋z＝－25，x、y、z皆为非负数，记整式5x+4y+z的最大值为a，最小值为b，则a﹣b =.

查看试题解析

三、解答题

17. 解三元一次方程组：

(1)、 ${\begin{matrix} 3 x - y + z = 4 \\ 2 x + 3 y - z = 12 \\ x + y + z = 6 \end{matrix}$

(2)、 ${\begin{matrix} x + z - 3 = 0 \\ 2 x - y + 2 z = 2 \\ x - y - z = - 3 \end{matrix}$ ．

查看试题解析
18. 解方程组 ${\begin{matrix} 4 x - 9 z = 17 \\ 3 x + y + 15 z = 18, \\ x + 2 y + 3 z = 2, \end{matrix}$ 并求出使等式ax+y+3z=0成立的a的值．

查看试题解析
19. 甲乙两人共有30本文艺书，乙丙两人共有50本文艺书，甲、丙两人共有40本文艺书，甲乙丙三人各有文艺书多少本?

查看试题解析
20. 一个三位数，如果把它的个位数字与百位数字交换位置，那么所得的新数比原数小99，且各位数字之和为14，十位数字是个位数字与百位数字之和．求这个三位数．

查看试题解析
21. 有一场足球比赛，共有九支球队参加，采取单循环赛，其记分和奖励方案如下表：

标准

胜一场

平一场

负一场

积分

3

1

0

奖励（元／人）

2000

800

0

甲队参加完了全部8场比赛，共得积分16分．

(1)、求甲队胜负的所有可能情况；

(2)、若每一场比赛，每一个参赛队员均可得出场费500元，求甲队参加了所有8场比赛的队员的个人总收入（奖金加上出场费）．

查看试题解析
22. 解二元一次方程组的关键是“消元”，即把“二元”转化为“一元”，同样，我们可以用“消元”的方法解三元一次方程组．下面，我们就来解一个三元一次方程组：
解方程组 ${\begin{array}{l} x + y + z = 2 ， ① \\ 2 x + 3 y - z = 8 ， ② \\ 3 x - 2 y + z = 3 ， ③ \end{array}$
小曹同学的部分解答过程如下：
解：______+______，得3x+4y=10，④
______+______，得5x+y=11，⑤
______与______联立，得方程组
${\begin{array}{l} 3 x + 4 y = 10 \\ 5 x + y = 11 \end{array}$

(1)、请你在方框中补全小曹同学的解答过程：

(2)、若m、n、p、q满足方程组 ${\begin{array}{l} m + n + p + q = 4 \\ 2 (m + n) + 3 p - q = 16 \\ 3 (m + n) - 2 p + q = 6 \end{array}$ ，则m+n-2p+q= ．

查看试题解析
23. 某货运公司接到 $120$ 吨物资运载任务，现有甲、乙、丙三种车型的汽车供选择，每辆车的运载能力和运费如表：

车型

甲

乙

丙

汽车运载量(吨/辆)

5

8

10

汽车运费(元/辆)

400

500

600

(1)、甲种车型的汽车 $2$ 辆，乙种车型的汽车 $3$ 辆，丙种车型的汽车 $4$ 辆，它们一次性能运载吨货物．

(2)、若全部物资都用甲、乙两种车型的汽车来运送，需运费 $8200$ 元，求需要甲、乙两种车型的汽车各多少辆？

(3)、为了节省运费，该公司打算用甲、乙、丙三种车型的汽车共 $15$ 辆同时参与运送，请你帮货运公司设计派车方案；并求出各种派车方案的运费．

查看试题解析

24. 一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	$5$	$8$	$10$
汽车运费（元/辆）	$400$	$500$	$600$

(1)、若全部物资都用甲、乙两种车型来运送，需运费

8200

元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知他们的总辆数为

16

辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

(3)、求出哪种方案的运费最省？最省是多少元？

查看试题解析

标准	胜一场	平一场	负一场
积分	3	1	0
奖励（元／人）	2000	800	0

车型	甲	乙	丙
汽车运载量(吨/辆)	5	8	10
汽车运费(元/辆)	400	500	600