初中数学浙教版八年级下学期期中复习专题7 分析数据的离散程度

试卷更新日期：2021-04-07 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 数据201，202，198，199，200的方差与极差分别是（   ）
    A、1，4 B、2，2 C、2，4 D、4，2

    查看试题解析

  • 2. 已知：甲乙两组数据的平均数都是5，甲组数据的方差S甲2＝ 6 ，乙组数据的方差S乙2＝2 2 ，下列结论中正确的是（   ）
    A、甲组数据比乙组数据的波动大 B、乙组数据比甲组数据的波动大 C、甲组数据与乙组数据的波动一样大 D、甲乙两组数据的波动大小不能比较

    查看试题解析

  • 3. 在“开学考试”，“第1次月考”，“第2次月考”这三次考试中，小西，小南两名同学的数学平均分都是120分，小西数学成绩的方差是15，小南数学成绩的方差是3，则下列说法正确的是（   ）
    A、小西的成绩比小南稳定 B、小南的成绩比小西稳定 C、小西，小南成绩一样稳定 D、无法确定谁的成绩更稳定

    查看试题解析

  • 4. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次测试的平均成绩都是125分，方差分别是 S甲2=0.65 ， S乙2=0.55 ， S丙2=0.50 ， S丁2=0.45 ，则这五次测试成绩最稳定的是（ ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 5. 为了了解七年级女生的跳绳情况，从中随机抽取了50女生进行1min跳绳测验，得到了这50名女生的跳绳成绩（单位：次），其中最小值为60，最大值为140，若取组距为15，则可分为（    ）
    A、7组 B、6组 C、5组 D、4组

    查看试题解析

  • 6. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表：

    选手

    甲

    乙

    丙

    丁

    平均数（环）

    9.2

    9.2

    9.2

    9.2

    方差（环2）

    0.35

    0.15

    0.25

    0.27

    则这四个中，成绩发挥最稳定的是（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 7. 某班5个合作学习小组人数如下：4，5，x，6，7，已知这数据的平均数为6，则这组数据的方差是（  ）
    A、2.9 B、2.8 C、2 D、3

    查看试题解析

  • 8. 如图是根据某地4月上旬每天最低气温绘成的折线图，那么这段时间最低气温的极差、众数、平均数依次是（  ）．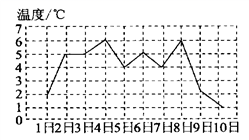

    A、5°  5°  4° B、5°  5°  4.5° C、2.8°  5°  4° D、2.8°  5°  4.5°

    查看试题解析

  • 9. 一组数据 x1,x2,⋅⋅⋅,xn 的方差是2，那么另一组数据 x1+3,x2+3,⋯,xn+3 的方差是（    ）
    A、2 B、3 C、4 D、5

    查看试题解析

  • 10. 如果将一组数据中的每个数都减去5，那么所得的一组新数据（    ）
    A、众数改变，方差改变 B、众数不变，平均数改变 C、中位数改变，方差不变 D、中位数不变，平均数不变

    查看试题解析

  • 11. 在样本方差的计算公式 S2=110[(x1−20)2+(x2−20)2+...+(x1−20)2] 中，数字10和20分别表示样本的（    ）
    A、容量和方差 B、标准差和平均数 C、容量和平均数 D、平均数和容量

    查看试题解析

二、填空题

  • 12. 甲、乙两射击运动员相同次数射击训练成绩的平均数和方差分别为 x甲¯=x乙¯=8 ， s2甲=1.1 ， s2乙=48 ，则成绩较为稳定的运动员是 ．

    查看试题解析

  • 13. 有一组数据如下：2，3，a，5，6，它们的平均数是4，则这组数据的方差是.

    查看试题解析

  • 14. 下图为甲、乙10次射击训练成绩的折线统计图。这些成绩的方差的大小关系是：S2甲S2乙。(选填“>”“=”“<”)

    查看试题解析

  • 15. 小明用 s2=110[(x1−6)2+(x2−6)2+⋅⋅⋅+(x10−6)2] 计算一组数据的方差，那么 x1+x2+x3+⋅⋅⋅+x10= ．

    查看试题解析

  • 16. 已知：一组数据 a ， b ， c ， d ， e 的平均数是22，方差是13，那么另一组数据 3a−2 ， 3b−2 ， 3c−2 ， 3d−2 ， 3e−2 的方差是.

    查看试题解析

  • 17. 已知样本数据为3，4，2，1，5，则标准差是 。

    查看试题解析

三、综合题

  • 18. 2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：

    成绩

    85

    90

    95

    100

    甲班参赛学生/人

    1

    1

    5

    3

    乙班参赛学生/人

    1

    2

    3

    4

    分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．

    查看试题解析

  • 19. 一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩有如下信息：
     

    A

    B

    C

    D

    E

    平均分

    标准差

    数学

    71

    72

    69

    68

    70

    		  

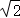
    英语

    88

    82

    94

    85

    76

    85

    		  
    (1)、求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
    (2)、为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式：标准分＝个人成绩﹣平均成绩）÷成绩标准差.

    从标准分看，标准分高的考试成绩更好，请问A同学在本次考试中，数学、英语哪个学科考得更好？

    查看试题解析

  • 20. A，B两家酒店规模相当，去年下半年的月盈利折线统计图如图所示。

    (1)、要评价这两家酒店7~12月的月盈利的平均水平，你选择什么统计量？求出这个统计量。
    (2)、已知A，B两家酒店7~12月的月盈利的方差分别为1.073(平方万元)，0.54(平方万元)。根据所给的方差和你在(1)中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由。

    查看试题解析

  • 21. 疫情期间，各小区进出人员都严格管控，实行实名登记、某周甲、乙两个小区周一至周五来访人数统计如下图：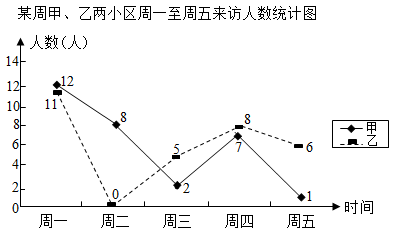

    (1)、请分别计算甲、乙两个小区每天来访人数的平均数.
    (2)、通过计算说明哪个小区来访人数比较稳定.

    查看试题解析

  • 22. 某中学开展演讲比赛活动，八年级(1)班、八年级(2)班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分100分)如下图：八年级(1)班成绩为条形统计图，八年级(2)班成绩为扇形统计图．

    (1)、根据上图填写下表

    班别

    平均数(分)

    中位数(分)

    众数(分)

    八年级(1)班

    85

    85

    八年级(2)班

    85

    80

    (2)、如果要在复赛成绩的十名选手中决定在同一班中选五名参加比赛活动，你认为哪个班实力更强一些？通过计算，说明理由．

    查看试题解析

  • 23. 如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥，它用粗大的钢索将桥面拉住，为检测钢索的抗拉强度，桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测，数据统计如下（单位：百吨）

    甲、乙两厂钢索抗拉强度检测统计表

    钢索

    1

    2

    3

    4

    5

    平均数

    中位数

    方差

    甲厂

    10

    11

    9

    10

    12

    10.4

    10

    1.04

    乙厂

    10

    8

    12

    7

    13

    a

    b

    c

    (1)、求乙厂5根钢索抗拉强度的平均数a（百吨）、中位数b（百吨）和方差c（平方百吨）.
    (2)、桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量，问哪一家的钢索质量更优？

    查看试题解析

  • 24.    8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）.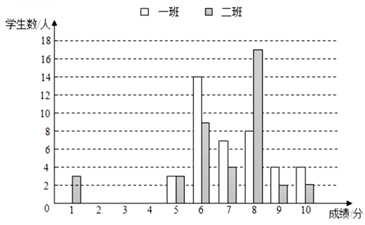

    班级

    平均分

    方差

    中位数

    众数

    合格率

    优秀率

    一班

    a

    2.11

    7

    c

    92.5%

    20%

    二班

    6.85

    4.28

    b

    8

    d

    10%

    根据图表信息，回答问题：

    (1)、直接写出表中a，b，c，d的值；
    (2)、用方差推断，班的成绩波动较大；用优秀率和合格率推断，班的阅读水平更好些；
    (3)、甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些。你认为谁的推断比较科学合理，更客观些，为什么？

    查看试题解析