初中数学浙教版七年级下学期期中复习专题5 二元一次方程（组）

试卷更新日期：2021-04-06 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知 $x^{2 m - 1} + 3 y^{4 - 2 n} = 7$ 是关于x，y的二元一次方程，则m，n的值为（）.

A、m=2，n=1 B、m=1，n= $- \frac{3}{2}$ C、m=1，n= $\frac{5}{2}$ D、m=1，n= $\frac{3}{2}$

查看试题解析
2. 二元一次方程2 x－y =1有无数多个解，下列四组值中是该方程的解的是（）

A、 ${\begin{matrix} x = 0 \\ y = 10.5 \end{matrix}$ B、 ${\begin{matrix} x = 4 \\ y = 7 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 11 \end{matrix}$ D、 ${\begin{matrix} x = 15 \\ y = 11 \end{matrix}$

查看试题解析
3. 已知二元一次方程组 ${\begin{matrix} m x + y = 0 \\ x + n y = 3 \end{matrix}$ 的解是 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ ，则 $m + 2 n$ 的值是（）

A、1 B、2 C、3 D、0

查看试题解析
4. 下列方程组中不是二元一次方程组的是（）

A、 ${\begin{cases} s + 1 = 3 \\ 2 s - t = 4 \end{cases}$ B、 ${\begin{cases} m + n = 3 \\ 2 m - n = 4 \end{cases}$ C、 ${\begin{cases} x = 3 \\ y = 4 \end{cases}$ D、 ${\begin{cases} x + y = 3 \\ 2 x y - y = 4 \end{cases}$

查看试题解析
5. 关于 $a$ 、 $b$ 的方程组 ${\begin{array}{l} a + 2 b = m \\ a + 3 b = m + 2 \end{array}$ 的解 $a$ 、 $b$ 互为负倒数，则 $m$ 的值为（）

A、1.5 B、2.5 C、3.5 D、4.5

查看试题解析
6. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{array}$ ，则下列结论中正确的是（）
①当a＝5时，方程组的解是 ${\begin{array}{l} x = 10 \\ y = 20 \end{array}$ ；②当x，y的值互为相反数时，a＝20；③当 $2^{x} \cdot 2^{y} = 16$ 时，a＝18；④不存在一个实数a使得x=y.

A、①②④ B、②③④ C、②③ D、②④

查看试题解析
7. 已知方程组 ${\begin{cases} \end{cases} \begin{matrix} 2 x - y = 4 \\ x - 2 y = m \end{matrix}$ 中的 $x$ ， $y$ 互为相反数，则 $m$ 的值为（）

A、 $2$ B、 $- 2$ C、 $0$ D、 $4$

查看试题解析
8. 已知 $| 5 x + 2 y - 13 | + {(3 x - y - 10)}^{2} = 0$ ，则 $y^{x}$ 的立方根为（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
9. 4辆板车和5辆卡车一次能运27吨货，10辆板车和3车卡车一次能运货20吨，设每辆板车每次可运x吨货，每辆卡车每次能运y吨货，则可列方程组（）

A、 ${\begin{array}{l} 4 x + 5 y = 27 \\ 10 x - 3 y = 20 \end{array}$ B、 ${\begin{array}{l} 4 x - 5 y = 27 \\ 10 x + 3 y = 20 \end{array}$ C、 ${\begin{array}{l} 4 x + 5 y = 27 \\ 10 x + 3 y = 20 \end{array}$ D、 ${\begin{array}{l} 4 x - 27 = 5 y \\ 10 x - 20 = 3 y \end{array}$

查看试题解析
10. 如图，将长与宽比为3：2的长方形ABCD分割成一个阴影长方形和由196个面积相等的小正方形构成的边框，（边框的宽度即为小正方形的边长），则阴影长方形的长与宽的比为（）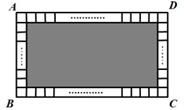

A、3：2 B、29：19 C、29：17 D、29：21

查看试题解析

二、填空题

11. 若关于x，y的方程 $(m - 1) x^{| m |} - y = 2$ 是一个二元一次方程，则m的值为.

查看试题解析
12. 若方程2x^2a^＋^b^－⁴＋4y^3a^－^2b^－³＝1是关于x，y的二元一次方程，则a＝， b＝.

查看试题解析
13. 已知 $a + 2 b = \frac{10}{3}$ ， $3 a + 4 b = \frac{16}{3}$ ，则a+b的值为.

查看试题解析
14. 若关于 $x, y$ 的方程组 ${\begin{array}{l} x + 2 y = 7 + k \\ 5 x - y = k \end{array}$ 的解互为相反数，则k = ．

查看试题解析
15. 如果方程组 ${\begin{array}{l} x = 2 \\ b x + a y = 5 \end{array}$ 的解与方程组 ${\begin{array}{l} y = 4 \\ b y + a x = 1 \end{array}$ 的解相同，则 $a + b$ 的值为．

查看试题解析
16. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第七卷《盈不足》记载了一道有趣的数学问题：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？” 译文：“今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问大容器、小容器的容量各是多少斛？”（注：斛，音hú，古量器名，亦是容量单位）设大容器的容量为 $x$ 斛，小容器的容量为 $y$ 斛，根据题意，可列方程组为．

查看试题解析

三、解答题

17. 解方程组

(1)、 ${\begin{matrix} 2 x - y = - 4 \\ 4 x - 5 y = - 23 \end{matrix}$ ；

(2)、 ${\begin{matrix} 3 (x - 1) = y + 5 \\ \frac{x + 2}{2} = \frac{y - 1}{3} + 1 \end{matrix}$

查看试题解析
18. 关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} x + 3 y = 2 k \\ x - y = 5 k \end{array}$ 的解也是二元一次方程 $x + 2 y = 11$ 的解，求 $k$ 的值.

查看试题解析
19. 甲、乙两人共同解方程组 ${\begin{matrix} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{matrix}$ ，由于甲看错了方程①中的a，得到方程组的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ；乙看错了方程②中的b，得到方程组的解为 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ，试计算a²⁰¹⁸+（﹣ $\frac{1}{10}$ b）²⁰¹⁷的值．

查看试题解析
20. 本地某快递公司规定：寄件不超过 $1$ 千克的部分按起步价计费；寄件超过 $1$ 千克的部分按千克计费.小丽分别寄快递到上海和北京，收费标准及实际收费如下表：
收费标准

目的地

起步价（元）

超过 $1$ 千克的部分

（元 $/$ 千克）

上海

$a$

$b$

北京

$a + 3$

$b + 4$

实际收费

目的地

质量

费用（元）

上海

2

9

北京

3

22

求 $a$ ， $b$ 的值.

查看试题解析
21. 已知关于x，y的二元一次方程组 ${\begin{cases} 2 x + 3 y = 1 \\ x - 2 y = 4 \end{cases}$ .

(1)、解该方程组；

(2)、若上述方程组的解是关于x，y的二元一次方程ax+by＝2的一组解，求代数式2b﹣4a的值.

查看试题解析
22. （阅读材料）小明同学遇到下列问题：解方程组 ${\begin{matrix} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{matrix}$ ，他发现如果直接用代入消元法或加减消元法求解，运算量比较大，也容易出错.如果把方程组中的 $(2 x + 3 y)$ 看作一个数，把 $(2 x - 3 y)$ 看作一个数，通过换元，可以解决问题.以下是他的解题过程：令 $m = 2 x + 3 y$ ， $n = 2 x - 3 y$ ，这时原方程组化为 ${\begin{matrix} \frac{m}{4} + \frac{n}{3} = 7 \\ \frac{m}{3} + \frac{n}{2} = 8 \end{matrix}$ ，解得 ${\begin{matrix} m = 60 \\ n = - 24 \end{matrix}$ ，把 ${\begin{matrix} m = 60 \\ n = - 24 \end{matrix}$ 代入 $m = 2 x + 3 y$ ， $n = 2 x - 3 y$ ，得 ${\begin{matrix} 2 x + 3 y = 60 \\ 2 x - 3 y = - 24 \end{matrix}$ ，解得 ${\begin{matrix} x = 9 \\ y = 14 \end{matrix}$ 所以，原方程组的解为 ${\begin{matrix} x = 9 \\ y = 14 \end{matrix}$
（解决问题）请你参考小明同学的做法，解决下面的问题：

(1)、解方程组 ${\begin{matrix} \frac{x + y}{3} + \frac{x - y}{5} = 2 \\ \frac{x + y}{3} - \frac{x - y}{5} = - 1 \end{matrix}$

(2)、已知方程组 ${\begin{matrix} a x + b y = m \\ c x + d y = n \end{matrix}$ 的解是 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ，直接写出方程组 ${\begin{matrix} a (x + 1) - b y = m \\ a (x + 1) - d y = n \end{matrix}$ 的解：.

查看试题解析
23. 某市准备安装完成5700辆共享单车投人市场．由于抽调不出足够熟练工人，公司准备招聘一批新工人．生产开始后发现：
1名熟练工人和2名新工人每天共安装28辆共享单车：2名熟练工人每天装的共享单车数与3名新工人每天安装的共享单车数一样多。

(1)、求每名熟练工人和新工人每天分别可以安装多少辆共享单车；

(2)、若公司原有熟练工a人，现招聘n名新工人（a>n），使得最后能刚好一个月（30天）完成安装任务，已知工人们安装的共享单车中不能正常投人运营的占5%，用含a的代数式表示n；

(3)、直接写出符合题意的n值。

查看试题解析
24. 如图1是某机场的平地电梯，电梯AB的长度为120米，如图2所示.若两人不乘电梯在地面匀速行走，小明每分钟的路程是小王的1.5倍，且1.5分钟后，小明比小王多行走30米.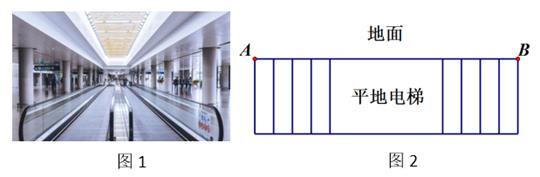

(1)、求两人在地面上每分钟各行走多少米？

(2)、若两人在平地电梯上行走，电梯向前行驶，两人也同时在电梯上行走.当小明到达B处时，小王还剩 $\frac{80}{3}$ 米.
①求平地电梯每分钟行驶多少米？

②当小明到达B处时，发现有一袋行李忘在A处，同时关注此时为7点55分，小明马上从地面返回A处，拿了行李后立即乘平地电梯（同时行走）去B处.问小明能否在8点前和小王汇合，并说明理由.

查看试题解析

目的地	质量	费用（元）
上海	2	9
北京	3	22