2015-2016学年河南省新乡市高一下学期期末数学试卷

试卷更新日期：2016-09-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列选项中小于tan $\frac{π}{6}$ 的是（）

A、sin $\frac{π}{4}$ B、cos $\frac{π}{3}$ C、sin $\frac{π}{2}$ D、cos $\frac{π}{6}$

查看试题解析
2. 下列各组向量中能作为表示它们所在平面内的所有向量的基底的是（）

A、 $\vec{a}$ =（0，0）， $\vec{b}$ =（1，﹣2） B、 $\vec{a}$ =（3，2）， $\vec{b}$ =（6，4） C、 $\vec{a}$ =（﹣1，2）， $\vec{b}$ =（5，7） D、 $\vec{a}$ =（﹣3，﹣1）， $\vec{b}$ =（3，1）

查看试题解析
3. 从甲、乙、丙、丁四人任选两人参加问卷调查，则甲被选中的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
4. 若2弧度的圆心角所夹的扇形的面积是4cm² ，则该圆心角所对的弧长为（）

A、2πcm B、2cm C、4πcm D、4cm

查看试题解析
5. 某程序框图如图所示，该程序运行后输出的k的值是（）

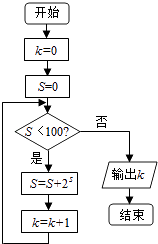A、4 B、5 C、6 D、7

查看试题解析
6. 函数y=2sin²（x﹣ $\frac{π}{4}$ ）﹣1是（）

A、最小正周期为π的奇函数 B、最小正周期为2π的奇函数 C、最小正周期为π的偶函数 D、最小正周期为2π的偶函数

查看试题解析
7. 设D为△ABC所在平面内一点，且 $\vec{B D}$ =3 $\vec{C D}$ ，则（）

A、 $\vec{A D}$ =﹣ $\frac{1}{3}$ $\vec{A B}$ + $\frac{4}{3}$ $\vec{A C}$ B、 $\vec{A D}$ = $\frac{4}{3}$ $\vec{A B}$ ﹣ $\frac{1}{3}$ $\vec{A C}$ C、 $\vec{A D}$ = $\frac{3}{2}$ $\vec{A B}$ ﹣ $\frac{1}{2}$ $\vec{A C}$ D、 $\vec{A D}$ =﹣ $\frac{1}{2}$ $\vec{A B}$ + $\frac{3}{2}$ $\vec{A C}$

查看试题解析
8. 为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：
收入x （万元）
8.2
8.6
10.0
11.3
11.9
支出y （万元）
6.2
7.5
8.0
8.5
9.8
据上表得回归直线方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ，其中 $\hat{b}$ =0.76， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b}$ $\bar{x}$ ，据此估计，该社区一户收入为15万元家庭年支出为（）

A、11.4万元 B、11.8万元 C、12.0万元 D、12.2万元

查看试题解析
9. 某中学初中部共有110名教师，高中部共有150名教师，其性别比例如图所示，则该校女教师的人数为（）

A、93 B、123 C、137 D、167

查看试题解析
10. 向量 $\vec{a}$ =（cosx， $\sqrt{2}$ +sinx）在向量 $\vec{b}$ =（1，1）方向上的投影的最大值为（）

A、1 B、 $\sqrt{2}$ ﹣1 C、1+ $\sqrt{2}$ D、2

查看试题解析
11. 秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法，对于求一个n次多项式函数f_n（x）=a_nxⁿ+a_n_﹣₁xⁿ^﹣¹+…+a₁x+a₀的具体函数值，运用常规方法计算出结果最多需要n次加法和 $\frac{n (n + 1)}{2}$ 乘法，而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法．对于计算机来说，做一次乘法运算所用的时间比做一次加法运算要长得多，所以此算法极大地缩短了CPU运算时间，因此即使在今天该算法仍具有重要意义．运用秦九韶算法计算f（x）=0.5x⁶+4x⁵﹣x⁴+3x³﹣5x当x=3时的值时，最先计算的是（）

A、﹣5×3=﹣15 B、0.5×3+4=5.5 C、3×3³﹣5×3=66 D、0.5×3⁶+4×3⁵=1336.6

查看试题解析
12. 若动直线x=a与函数f（x）= $\sqrt{3}$ sin（x+ $\frac{π}{6}$ ）和g（x）=sin（ $\frac{π}{3}$ ﹣x）的图象分别交于M，N两点，则|MN|的最大值为（）

A、1 B、2 C、 $\sqrt{3}$ D、1+ $\sqrt{3}$

查看试题解析

二、填空题

13. sin40°cos10°+cos140°sin10°= ．

查看试题解析
14. 某校为了了解学生对周末家庭作业量的态度，拟采用分层抽样的方法分别从高一、高二、高三的高中生中随机抽取一个容量为200的样本进行调查，已知从700名高一、高二学生中共抽取了140名学生，那么该校有高三学生名．

查看试题解析
15. 已知集合M={x|0＜x≤6}，从集合M中任取一个数x，使得函数y=log₂x的值大于1的概率为．

查看试题解析
16. 给出下列命题：
①存在实数x，使sinx+cosx= $\frac{3}{2}$ ；
②若α，β是第一象限角，且α＞β，则cosα＜cosβ；
③函数y=sin（ $\frac{2}{3}$ x+ $\frac{π}{2}$ ）是偶函数；
④函数y=sin2x的图象向左平移 $\frac{π}{4}$ 个单位，得到函数y=cos2x的图象．
其中正确命题的序号是（把正确命题的序号都填上）

查看试题解析

三、解答题

17. 已知 $\vec{a}$ 与 $\vec{b}$ 均为单位向量，它们的夹角为60°．

(1)、求| $\vec{a}$ ﹣3 $\vec{b}$ |

(2)、若x $\vec{a}$ ﹣ $\vec{b}$ 与 $\vec{a}$ +x $\vec{b}$ 垂直，求x的值．

查看试题解析
18. 在某次测验中，有6位同学的平均成绩为75分．用x_n表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学同学的成绩如表：
n
1
2
3
4
5
x₀
70
76
72
70
72

(1)、求第6位同学的成绩x₆及这6位同学成绩的标准差s；

(2)、若从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间[68，75）中的概率．

查看试题解析
19. 化简求值：

(1)、 $\frac{\sqrt{1 - 2 \sin 100^{\circ} \cos 280^{\circ}}}{\cos 370^{\circ} - \sqrt{1 - \cos^{2} 170^{\circ}}}$

(2)、tan20°+4sin20°．

查看试题解析
20. 随机抽取一个年份，对西安市该年4月份的天气情况进行统计，结果如下：

(1)、在4月份任取一天，估计西安市在该天不下雨的概率；

(2)、西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会，估计运动会期间不下雨的概率．
日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
天气
晴
雨
阴
阴
阴
雨
阴
晴
晴
晴
阴
晴
晴
晴
晴
日期
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
天气
晴
阴
雨
阴
阴
晴
阴
晴
晴
晴
阴
晴
晴
晴
雨

查看试题解析
21. 已知点A（2sinx，﹣cosx）、B（ $\sqrt{3}$ cosx，2cosx），记f（x）= $\vec{O A}$ • $\vec{O B}$ ．

(1)、若x₀是函数y=f（x）﹣1的零点，求tanx₀的值；

(2)、求f（x）在区间[ $\frac{π}{6}$ ， $\frac{π}{2}$ ]上的最值及对应的x的值．

查看试题解析
22. 某海滨浴场每年夏季每天的海浪高度y（米）是时间x（0≤x≤24，单位：小时）的函数，记作y=f（x），下表是每年夏季每天某些时刻的浪高数据：
x（时）
0
3
6
9
12
15
18
21
24
y（米）
1.5
1.0
0.5
1.0
1.5
1.0
0.5
1.0
1.5

(1)、经观察发现可以用三角函数y=Acosωx+b对这些数据进行拟合，求函数f（x）的表达式；

(2)、浴场规定，每天白天当海浪高度高于1.25米时，才对冲浪爱好者开放，求冲浪者每天白天可以在哪个时段到该浴场进行冲浪运动？

查看试题解析

收入x （万元）	8.2	8.6	10.0	11.3	11.9
支出y （万元）	6.2	7.5	8.0	8.5	9.8

日期	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
天气	晴	雨	阴	阴	阴	雨	阴	晴	晴	晴	阴	晴	晴	晴	晴

x（时）	0	3	6	9	12	15	18	21	24
y（米）	1.5	1.0	0.5	1.0	1.5	1.0	0.5	1.0	1.5

n	1	2	3	4	5
x₀	70	76	72	70	72