2015-2016学年广东省汕头市高一下学期期末数学试卷

试卷更新日期：2016-09-20 类型：期末考试

进入出卷网下载

一、选择题

1. 设集合A={x|0＜x＜2}，B={x|x²+x﹣2≥0}，则A∩B=（）

A、（0，1] B、[1，2） C、[﹣2，2） D、（0，2）

查看试题解析
2. sin160°cos10°+cos20°sin10°=（）

A、 $- \frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析
3. 下列函数中，在其定义域内既是奇函数又是减函数的是（）

A、y=x³ ， x∈R B、y=sinx，x∈R C、y=﹣x，x∈R D、y=（ $\frac{1}{2}$ ）^x ， x∈R

查看试题解析
4. 已知 $\vec{a}$ ⊥ $\vec{b}$ ，并且 $\vec{a}$ =（3，x）， $\vec{b}$ =（7，12），则x=（）

A、﹣ $\frac{7}{4}$ B、 $\frac{7}{4}$ C、﹣ $\frac{7}{3}$ D、 $\frac{7}{3}$

查看试题解析
5. 若tanα= $\frac{4}{3}$ ，则cos2α等于（）

A、 $\frac{7}{25}$ B、﹣ $\frac{7}{25}$ C、1 D、 $\frac{\sqrt{7}}{5}$

查看试题解析
6. 某市重点中学奥数培训班共有14人，分为两个小组，在一次阶段考试中两个小组成绩的茎叶图如图所示，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则m+n的值是（）

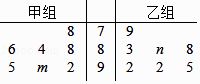A、10 B、11 C、12 D、13

查看试题解析
7. 已知0＜x＜y＜a＜1，则有（）

A、log_a（xy）＜0 B、0＜log_a（xy）＜1 C、1＜log_a（xy）＜2 D、log_a（xy）＞2

查看试题解析
8. 要得到y=sin（﹣2x+ $\frac{π}{4}$ ）的图象，只需将y=sin（﹣2x）的图象（）

A、向左平移 $\frac{π}{4}$ 个单位 B、向右平移 $\frac{π}{4}$ 个单位 C、向左平移 $\frac{π}{8}$ 个单位 D、向右平移 $\frac{π}{8}$ 个单位

查看试题解析
9. 已知平面向量 $\vec{a}$ 、 $\vec{b}$ 满足：2| $\vec{a}$ |=| $\vec{b}$ |=|2 $\vec{a}$ ﹣ $\vec{b}$ |≠0，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{6}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
10.
如果执行如图所示的框图，输入N=5，则输出的数等于（）

A、 $\frac{5}{4}$ B、 $\frac{4}{5}$ C、 $\frac{6}{5}$ D、 $\frac{5}{6}$

查看试题解析
11. 已知a，b均为正数，且a+b=1，则 $\frac{4}{a}$ + $\frac{9}{b}$ 的最小值为（）

A、24 B、25 C、26 D、27

查看试题解析
12. 已知x∈R，用A（x）表示不小于x的最小整数，如A（ $\sqrt{3}$ ）=2，A（﹣1，2）=﹣1，若A（2x+1）=3，则x的取值范围是（）

A、[1， $\frac{3}{2}$ ） B、（1， $\frac{3}{2}$ ] C、[ $\frac{1}{2}$ ，1） D、（ $\frac{1}{2}$ ，1]

查看试题解析

二、填空题

13. 高一（4）班有5位同学参加夏令营植树活动，其中男生2人，女生3人，从这5人中任意选出2人去浇水，选出的2人都是男生的概率是．

查看试题解析
14. 已知x，y满足不等式 ${\begin{matrix} x - 4 y \leq - 3 \\ 3 x + 5 y \leq 25 \\ x \geq 1 \end{matrix}$ ，且函数z=2x+y﹣a的最大值为8，则常数a的值为．

查看试题解析
15. 已知函数f（x）=asinxcosx﹣sin²x+ $\frac{1}{2}$ 的一条对称轴方程为x= $\frac{π}{6}$ ，则函数f（x）的最大值为．

查看试题解析
16. 定义一种运算a⊗b= ${\begin{matrix} a ， a \leq b \\ b ， a > b \end{matrix}$ ，令f（x）=（3x²+6x）⊗（2x+3﹣x²），则函数f（x）的最大值是．

查看试题解析

三、解答题

17. 已知S_n为等差数列{a_n}的前n项和，且a₁=﹣15，S₅=﹣55．

(1)、求数列{a_n}的通项公式；

(2)、若不等式S_n＞t对于任意的n∈N^*恒成立，求实数t的取值范围．

查看试题解析
18. 在△ABC中，角A、B、C所对的边分别是a、b、c，且满足csinA﹣ $\sqrt{3}$ acosC=0．

(1)、求角C的大小；

(2)、若c=2，求△ABC的面积S的最大值．

查看试题解析
19. 从某大学一年级女生中，选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名，其身高和体重数据如表所示：
身高/cm（x）
150
155
160
165
170
体重/kg（y）
43
46
49
51
56

(1)、求y关于x的线性回归方程；

(2)、利用（1）中的回归方程，计算身高为168cm时，体重的估计值 $\hat{y}$ 为多少？
参考公式：线性回归方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ，其中 $\hat{b}$ = $\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ = $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} X_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b}$ $\bar{x}$ ．

查看试题解析
20. 设函数f（x）=ax²﹣（a+1）x+1．

(1)、若不等式f（x）＜mx的解集为{x|1＜x＜2}，求实数a、m的值；

(2)、解不等式f（x）＜0．

查看试题解析
21. 已知 S_n是数列{a_n}的前n项和，且S_n=2a_n+n﹣4．

(1)、求a₁的值；

(2)、若b_n=a_n﹣1，试证明数列{b_n}为等比数列；

(3)、求数列{a_n}的通项公式，并证明： $\frac{1}{a_{1}}$ + $\frac{1}{a_{2}}$ +…+ $\frac{1}{a_{n}}$ ＜1．

查看试题解析
22. 对于函数y=f（x），若x₀满足f（x₀）=x₀ ，则称x₀为函数f（x）的一阶不动点，若x₀满足f[f（x₀）]=x₀ ，则称x₀为函数f（x）的二阶不动点，

(1)、设f（x）=2x+3，求f（x）的二阶不动点．

(2)、若f（x）是定义在区间D上的增函数，且x₀为函数f（x）的二阶不动点，求证：x₀也必是函数f（x）的一阶不动点；

(3)、设f（x）=e^x+x+a，a∈R，若f（x）在[0，1]上存在二阶不动点x₀ ，求实数a的取值范围．

查看试题解析

身高/cm（x）	150	155	160	165	170
体重/kg（y）	43	46	49	51	56