2015-2016学年安徽省黄山市高一下学期期末数学试卷

试卷更新日期：2016-09-19 类型：期末考试

进入出卷网下载

一、选择题

1. 不等式 $\frac{1}{x} < \frac{1}{2}$ 的解集是（）

A、（﹣∞，2） B、（2，+∞） C、（0，2） D、（﹣∞，0）∪（2，+∞）

查看试题解析
2. 设S_n为公差不为零的等差数列{a_n}的前n项和，若S₉=3a₈ ，则 $\frac{a_{8}}{a_{5}}$ =（）

A、3 B、5 C、7 D、21

查看试题解析
3. 如果a＞b＞0，且a+b=1，那么在不等式① $\frac{a}{b} < 1$ ；② $\frac{1}{b} < \frac{1}{a}$ ；③ $\frac{1}{b} + \frac{1}{a} < \frac{1}{a b}$ ；④ab $< \frac{1}{4}$ 中，一定成立的不等式的序号是（　　）

A、① B、② C、③ D、④

查看试题解析
4. 某校高三年级共有学生900人，编号为1，2，3，…，900，现用系统抽样的方法抽取一个容量为45的样本，则抽取的45人中，编号落在区间[481，720]的人数为（）

A、10 B、11 C、12 D、13

查看试题解析
5. 已知具有线性相关关系的两个变量x，y之间的一组数据如表：
x
0
1
2
3
4
y
2.2
4.3
4.5
4.8
6.7
且回归直线方程为 $\hat{y}$ =bx+2.6，根据模型预报当x=6时，y的预测值为（）

A、5.76 B、6.8 C、8.3 D、8.46

查看试题解析
6. 从标有1，2，3，4，5，6的6张纸片中任取2张，那么这2张纸片数字之积为6的概率是（　　）

A、 $\frac{1}{5}$ B、 $\frac{1}{15}$ C、 $\frac{2}{15}$ D、 $\frac{1}{3}$

查看试题解析
7. 某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9．已知这组数据的平均数为10，方差为2，则|x﹣y|的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知变量x，y满足： ${\begin{matrix} 2 x - y \leq 0 \\ x - 2 y + 3 \geq 0 \\ x \geq 0 \end{matrix}$ ，则z=（ $\sqrt{3}$ ）^2x+y的最大值为（）

A、 $\sqrt{3}$ B、3 $\sqrt{3}$ C、3 D、9

查看试题解析
9. 我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数x的不足近似值和过剩近似值分别为 $\frac{b}{a}$ 和 $\frac{d}{c}$ （a，b，c，d∈N^*），则 $\frac{b + d}{a + c}$ 是x的更为精确的不足近似值或过剩近似值．我们知道π=3.14159…，若令 $\frac{31}{10}$ ＜π＜ $\frac{49}{15}$ ，则第一次用“调日法”后得 $\frac{16}{5}$ 是π的更为精确的过剩近似值，即 $\frac{31}{10}$ ＜π＜ $\frac{16}{5}$ ，若每次都取最简分数，那么第四次用“调日法”后可得π的近似分数为（）

A、 $\frac{22}{7}$ B、 $\frac{63}{20}$ C、 $\frac{78}{25}$ D、 $\frac{109}{35}$

查看试题解析
10. 某调查机构对本市小学生课业负担情况进行了调查，设平均每人每天做作业的时间为x分钟．有1000名小学生参加了此项调查，调查所得数据用程序框图处理，若输出的结果是680，则平均每天做作业的时间在0～60分钟内的学生的频率是（）

A、680 B、320 C、0.68 D、0.32

查看试题解析
11. 在平面区域{（x，y）|0≤x≤1，1≤y≤2}内随机投入一点P，则点P的坐标（x，y）满足y≤2x的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 已知等比数列{a_n}的前n项和为S_n ，若a₂=12，a₃•a₅=4，则下列说法正确的是（）

A、{a_n}是单调递减数列 B、{S_n}是单调递减数列 C、{a_2n}是单调递减数列 D、{S_2n}是单调递减数列

查看试题解析

二、填空题

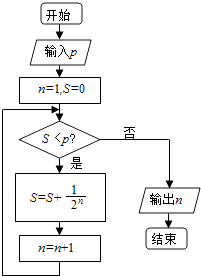
13. 若六进制数10k5_（₆_）（k为正整数）化为二进制数为11101111_（₂_），则k= ．

查看试题解析
14. 执行如图所示的程序框图，若p=0.8，则输出的n= ．

查看试题解析
15. 已知正数x，y满足x+y=1，则 $\frac{1}{x} + \frac{x}{y}$ 的最小值为．

查看试题解析
16. 已知f（m）=（3m﹣1）a+b﹣2m，当m∈[0，1]时，f（m）≤1恒成立，则a+b的最大值是．

查看试题解析

三、解答题

17. 已知f（x）=﹣3x²+a（6﹣a）x+b，a，b为实数．

(1)、当b=﹣6时，解关于a的不等式f（1）＞0；

(2)、若不等式f（x）＞0的解集为（﹣1，3），求实数a，b的值．

查看试题解析
18. 在△ABC中，A、B、C的对边分别为a、b、c，已知c﹣b=2bcosA．

(1)、若a=2 $\sqrt{6}$ ，b=3，求c；

(2)、若C= $\frac{π}{2}$ ，求角B．

查看试题解析
19. 甲、乙两位学生参加数学竞赛培训，在培训期间，他们参加的5次预赛成绩记录如下：
甲
    82
    82
    79
    95
    87
乙
    95
    75
    80
    90
    85

(1)、请用茎叶图表示这两组数据；

(2)、从甲、乙两人的成绩中各随机抽取一个，求甲的成绩比乙高的概率；

(3)、现要从中选派一人参加9月份的全国数学联赛，从统计学的角度考虑，你认为选派哪位学生参加合适？请说明理由．

查看试题解析
20. △ABC的三个内角A，B，C所对的边分别为a，b，c，向量 $\vec{m} = (- 1 ， 1)$ ， $\vec{n} = (\cos B \cos C ， \sin B \sin C - \frac{\sqrt{3}}{2})$ ，且 $\vec{m} ⊥ \vec{n}$ ．

(1)、求A的大小；

(2)、现在给出下列三个条件：①a=1；② $2 c - (\sqrt{3} + 1) b = 0$ ；③B=45°，试从中选择两个条件以确定△ABC，求出所确定的△ABC的面积．

查看试题解析
21. 某校对高一年级学生寒假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如图：
分组
频数
频率
[10，15）
20
0.25
[15，20）
50
n
[20，25）
m
p
[25，30）
4
0.05
合计
M
N

(1)、求表中n，p的值和频率分布直方图中a的值，并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数；

(2)、如果用分层抽样的方法从样本服务次数在[10，15）和[25，30）的人中共抽取6人，再从这6人中选2人，求2人服务次数都在[10，15）的概率．

查看试题解析
22. 各项均为正数的数列{a_n}中，a₁=1，S_n是数列{a_n}的前n项和，对任意n∈N^* ，有2S_n=2pa_n²+pa_n﹣p（p∈R）

(1)、求常数p的值；

(2)、求数列{a_n}的通项公式；

(3)、记b_n= $\frac{4 S_{n}}{n + 3} \cdot 2^{n}$ ，求数列{b_n}的前n项和T．

查看试题解析

分组	频数	频率
[10，15）	20	0.25
[15，20）	50	n
[20，25）	m	p
[25，30）	4	0.05
合计	M	N

x	0	1	2	3	4
y	2.2	4.3	4.5	4.8	6.7

甲	82	82	79	95	87
乙	95	75	80	90	85