2015-2016学年北京市房山区高三上学期期末数学试卷（理科）

试卷更新日期：2016-09-19 类型：期末考试

进入出卷网下载

一、选择题

1. 在复平面内，复数 $\frac{1}{2 + i}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在 ${(x + \frac{2}{x})}^{6}$ 的展开式中，常数项为（）

A、160 B、64 C、20 D、8

查看试题解析
3. 执行如图所示的程序框图，则输出S的值为（）

A、﹣10 B、6 C、8 D、14

查看试题解析
4. 如图，圆O的弦AB，CD相交于点E，过点A作圆O的切线与DC的延长线交于点P，若PA=6，AE=9，BE=2，ED=3，则PC=（）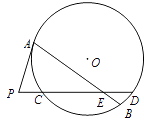

A、1 B、2 C、3 D、4

查看试题解析
5. “b＜a＜0”是“ $\frac{b}{a} + \frac{a}{b} > 2$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 若曲线x²+y²=r²经过不等式组 ${\begin{matrix} x + 2 y - 2 \leq 0 \\ 3 x + y - 3 \geq 0 \\ y \geq 0 \end{matrix}$ 表示的平面区域，则r的取值范围是（）

A、 $[\frac{9}{10} ， 4]$ B、 $[\frac{3 \sqrt{10}}{10} ， 2]$ C、[1，2] D、[1，4]

查看试题解析
7.
如图是一个几何体的三视图，则该几何体的体积等于（）

A、 $\frac{1}{2}$ B、 $\frac{5}{6}$ C、1 D、 $\frac{5}{3}$

查看试题解析
8. 将编号为1至12的12本书分给甲、乙、丙三人，每人4本．
甲说：我拥有编号为1和3的书；
乙说：我拥有编号为8和9的书；
丙说：我们三人各自拥有的书的编号之和相等．
据此可判断丙必定拥有的书的编号是（）

A、2和5 B、5和6 C、2和11 D、6和11

查看试题解析

二、填空题

9. 抛物线y²=2x的焦点坐标为．

查看试题解析
10. 向量 $\vec{e_{1}} ， \vec{e_{2}} ， \vec{a} ， \vec{b}$ 在正方形网格中的位置如图所示，若 $\vec{a} - \vec{b} = x \vec{e_{1}} + y \vec{e_{2}}$ ，则x= ， y= ．

查看试题解析
11. 在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρsinθ=1，曲线C的参数方程为 ${\begin{matrix} x = 2 \cos ϕ \\ y = 2 \sin ϕ \end{matrix}$ （ϕ为参数），l与C相交于A，B两点，则|AB|= ．

查看试题解析
12. 已知函数f（x）=sinxcosx，则f（x）的最小正周期为， f（x）在 $[- \frac{π}{8} ， \frac{π}{4}]$ 上的最小值为．

查看试题解析
13. 如图，定义在[﹣1，1]上的函数f（x）的图象为折线AOB．若方程f（x）﹣mx﹣m=0有两个不等的实根，则实数m的取值范围是．

查看试题解析
14. 已知非空集合M满足：∀a∈M，总有a²∉M且 $\sqrt{a} \notin M$ ．若M⊆{1，2}，则M=；若 $M \subseteq {x \in N | y = \sqrt{5 + 4 x - x^{2}}}$ ，则满足条件的M共有个．

查看试题解析

三、解答题

15. 在△ABC中，角A，B，C的对边分别为a，b，c，且a＜b＜c， $\sqrt{3} a = 2 b \sin A$ ．

(1)、求B的大小；

(2)、若a=2， $b = \sqrt{7}$ ，求c的值．

查看试题解析
16. 已知数列{a_n}（n=1，2，3，…）满足a_n+1=2a_n ，且a₁ ， a₂+1，a₃成等差数列，设b_n=3log₂a_n﹣7．

(1)、求数列{a_n}，{b_n}的通项公式；

(2)、求数列{|b_n|}的前n项和T_n ．

查看试题解析
17. 某校学生会为了了解学生对于“趣味运动会”的满意程度，从高一、高二两个年级分别随机调查了20个学生，得到学生对“趣味运动会”所设项目的满意度评分如下：
高一：62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
高二：73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79

(1)、根据两组数据完成两个年级满意度评分的茎叶图，并通过茎叶图比较两个年级满意度评分的平均值及离散程度（不要求计算出具体值，给出结论即可）；
高一
茎
高二
4
3
5
6
4
2
6
6
8
8
6
4
3
7
9
2
8
6
5
1
8
7
5
5
2
9

(2)、根据学生满意度评分，将学生的满意度从低到高分为三个等级：
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
假设两个年级的评价结果相互独立．根据所给数据，以事件发生的频率作为相应事件发生的概率．随机调查高一、高二各一名学生，记事件A：“高一、高二学生都非常满意”，事件B：“高一的满意度等级高于高二的满意度等级”．分别求事件A、事件B的概率．

查看试题解析
18. 如图1，在直角梯形ADCE中，AD∥EC，∠ADC=90°，AB⊥EC，AB=EB=1， $B C = \sqrt{2}$ ．将△ABE沿AB折到△ABE₁的位置，使∠BE₁C=90°．M，N分别为BE₁ ， CD的中点．如图2．

(1)、求证：MN∥平面ADE₁；

(2)、求证：AM⊥E₁C；

(3)、求平面AE₁N与平面BE₁C所成锐二面角的余弦值．

查看试题解析
19. 设函数f（x）=（x﹣a）e^x+（a﹣1）x+a，a∈R．

(1)、当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；

(2)、设g（x）=f′（x），证明：当a＞2时，函数g（x）在（0，+∞）上仅有一个零点；

(3)、若对任意的x∈[0，2]，恒有f（x）≤0成立，求实数a的取值范围．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{8} + \frac{y^{2}}{n} = 1$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，F是椭圆C的右焦点．过点F且斜率为k（k≠0）的直线l与椭圆C交于A，B两点，O是坐标原点．

(1)、求n的值；

(2)、若线段AB的垂直平分线在y轴的截距为 $\frac{2}{3}$ ，求k的值；

(3)、是否存在点P（t，0），使得PF为∠APB的平分线？若存在，求出t的值；若不存在，说明理由．

查看试题解析

满意度评分	低于70分	70分到89分	不低于90分
满意度等级	不满意	满意	非常满意

高一						茎	高二
						4
					3	5
			6	4	2	6
6	8	8	6	4	3	7
9	2	8	6	5	1	8
		7	5	5	2	9