2015-2016学年辽宁省五校协作体高二下学期期中数学试卷（理科）

试卷更新日期：2016-09-19 类型：期中考试

进入出卷网下载

一、选择题

1. 复数 $\frac{1}{- 2 + i} + \frac{1}{1 - 2 i}$ 的虚部是（）

A、 $\frac{1}{5}$ i B、 $\frac{1}{5}$ C、- $\frac{1}{5}$ i D、- $\frac{1}{5}$

查看试题解析
2. 直线y= $\frac{1}{2}$ x+b是曲线y=lnx的一条切线，则实数b的值为（）

A、2 B、ln2+1 C、ln2﹣1 D、ln2

查看试题解析
3. 袋中共有8个球，其中3个红球、2个白球、3个黑球．若从袋中任取3个球，则所取3个球中至多有1个红球的概率是（）

A、 $\frac{9}{14}$ B、 $\frac{37}{56}$ C、 $\frac{39}{56}$ D、 $\frac{5}{7}$

查看试题解析
4. 有八名运动员参加男子100米的决赛．已知运动场有从内到外编号依次为1，2，3，4，5，6，7，8的八条跑道，若指定的3名运动员所在的跑道编号必须是三个连续的数字（如：4，5，6），则参加比赛的这八名运动员安排跑道的方式共有（）

A、360种 B、4320种 C、720种 D、2160种

查看试题解析
5. 设（ $\frac{1}{x}$ +x²）³的展开式中的常数项为a，则直线y=ax与曲线y=x²围成图形的面积为（）

A、 $\frac{27}{2}$ B、9 C、 $\frac{9}{2}$ D、 $\frac{27}{4}$

查看试题解析
6. 设函数f（x）在R上可导，其导函数f′（x），且函数f（x）在x=﹣2处取得极小值，则函数y=xf′（x）的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 若z= $\frac{1}{2}$ + $\frac{\sqrt{3}}{2}$ i，且（x﹣z）⁴=a₀x⁴+a₁x³+a₂x²+a₃x+a₄ ，则a₂等于（）

A、﹣ $\frac{1}{2}$ + $\frac{\sqrt{3}}{2}$ i B、﹣3+3 $\sqrt{3}$ i C、6+3 $\sqrt{3}$ i D、﹣3﹣3 $\sqrt{3}$ i

查看试题解析
8. （|x|+ $\frac{1}{| x |}$ ﹣2）³的展开式中的常数项为（）

A、﹣20 B、19 C、﹣18 D、21

查看试题解析
9. 设f（x）是 ${(x^{2} + \frac{1}{2 x})}^{6}$ 展开式的中间项，若f（x）≤mx在区间[[ $\frac{\sqrt{2}}{2}$ ， $\sqrt{2}$ ]， $\sqrt{2}$ ]上恒成立，则实数m的取值范围是（）

A、（﹣∞，5） B、（﹣∞，5] C、（5，+∞） D、[5，+∞）

查看试题解析
10. 已知面积为S的凸四边形中，四条边长分别记为a₁ ， a₂ ， a₃ ， a₄ ，点P为四边形内任意一点，且点P到四边的距离分别记为h₁ ， _h2 ， h₃ ， h₄ ，若 $\frac{a_{1}}{1}$ = $\frac{a_{2}}{2}$ = $\frac{a_{3}}{3}$ = $\frac{a_{4}}{4}$ =k，则h₁+2h₂+3h₃+4h₄= $\frac{2 s}{k}$ 类比以上性质，体积为y的三棱锥的每个面的面积分别记为S_l ， S₂ ， S₃ ， S₄ ，此三棱锥内任一点Q到每个面的距离分别为H₁ ， H₂ ， H₃ ， H₄ ，若 $\frac{s_{1}}{1}$ = $\frac{s_{2}}{2}$ = $\frac{s_{3}}{3}$ = $\frac{s_{4}}{4}$ =K，则H₁+2H₂+3H₃+4H₄=（）

A、 $\frac{4 V}{k}$ B、 $\frac{3 V}{k}$ C、 $\frac{2 V}{k}$ D、 $\frac{V}{k}$

查看试题解析
11. 已知f（x）= ${\begin{matrix} x + 3 ， x \leq 1 \\ - x^{2} + 2 x + 3 ， x > 1 \end{matrix}$ ，则使得f（x）﹣e^x﹣m≤0恒成立的m的取值范围是（）

A、（﹣∞，2） B、（﹣∞，2] C、（2，+∞） D、[2，+∞）

查看试题解析
12. 已知a为常数，函数f（x）=x（lnx﹣ax）有两个极值点x₁ ， x₂（x₁＜x₂）（）

A、 $f (x_{1}) ＞ 0 ， f (x_{2}) ＞ - \frac{1}{2}$ B、 $f (x_{1}) ＜ 0 ， f (x_{2}) ＜ - \frac{1}{2}$ C、 $f (x_{1}) ＞ 0 ， f (x_{2}) ＜ - \frac{1}{2}$ D、 $f (x_{1}) ＜ 0 ， f (x_{2}) ＞ - \frac{1}{2}$

查看试题解析

二、填空题

13. 已知函数f（x）=a^xlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为

查看试题解析
14. 观察下列式子：1+ $\frac{1}{2^{2}}$ ＜ $\frac{3}{2}$ ，1+ $\frac{1}{2^{2}}$ + $\frac{1}{3^{2}}$ ＜ $\frac{5}{3}$ ，1+ $\frac{1}{2^{2}}$ + $\frac{1}{3^{2}}$ + $\frac{1}{4^{2}}$ ＜ $\frac{7}{4}$ ，…，根据以上式子可以猜想1+ $\frac{1}{2^{2}}$ + $\frac{1}{3^{2}}$ +…+ $\frac{1}{2014^{2}}$ ＜．

查看试题解析
15. 将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中．若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有种．

查看试题解析
16. 有以下命题：
①若f（x）=x³+（a﹣1）x²+3x+1没有极值点，则﹣2＜a＜4；
②集合M={1，2，zi}，i为虚数单位，N={3，4}，M∩N={4}，则复数z=﹣4i；
③若函数f（x）= $\frac{\ln x}{x}$ ﹣m有两个零点，则m＜ $\frac{1}{e}$ ．
其中正确的是．

查看试题解析

三、解答题：解答应写出文字说明，证明过程或演算步骤.

17. 当实数m为何值时，复数z= $\frac{m^{2} + m - 6}{m}$ +（m²﹣2m）i为

(1)、实数？

(2)、虚数？

(3)、纯虚数？

查看试题解析
18. 已知关于x的函数 $f (x) =- \frac{1}{3} x^{3} + b x^{2} + c x + b c$ ．

(1)、如果函数 $f (x) 在 x = 1 处有极值 - \frac{4}{3}$ ，求b、c；

(2)、设当x∈（ $\frac{1}{2}$ ，3）时，函数y=f（x）﹣c（x+b）的图象上任一点P处的切线斜率为k，若k≤2，求实数b的取值范围．

查看试题解析
19. 如图所示，抛物线y=1﹣x²与x轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在x轴上．已知工业用地每单位面积价值为3a元（a＞0），其它的三个边角地块每单位面积价值a元．

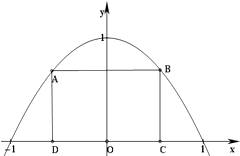(1)、求等待开垦土地的面积；

(2)、如何确定点C的位置，才能使得整块土地总价值最大．

查看试题解析
20. 已知函数f（x）=xlnx，g（x）=（﹣x²+ax﹣3）e^x（其中a实数，e是自然对数的底数）．

(1)、当a=5时，求函数y=g（x）在点（1，e）处的切线方程；

(2)、求f（x）在区间[t，t+2]（t＞0）上的最小值；

(3)、若存在x₁ ， x₂∈[e^﹣¹ ， e]（x₁≠x₂），使方程g（x）=2e^xf（x）成立，求实数a的取值范围．

查看试题解析
21. 已知（x+1）ⁿ=a₀+a₁（x﹣1）+a₂（x﹣1）²+a₃（x﹣1）³+…+a_n（x﹣1）ⁿ ，（其中n∈N^*）

(1)、求a₀及S_n=a₁+2a₂+3a₃+…+na_n；

(2)、试比较S_n与n³的大小，并说明理由．

查看试题解析
22. 已知函数f（x）= $\frac{\ln (x + 1)}{x}$ ．

(1)、判断f（x）在（0，+∞）的单调性；

(2)、若x＞0，证明：（e^x﹣1）ln（x+1）＞x² ．

查看试题解析