2012年高考理数真题试卷（福建卷）

试卷更新日期：2016-09-18 类型：高考真卷

进入出卷网下载

一、选择题：在每小题给出分四个选项中，只有一项是符合题目要求的．

1. 若复数z满足zi=1﹣i，则z等于（）

A、﹣1﹣I B、1﹣I C、﹣1+I D、1+i

查看试题解析
2. 等差数列{a_n}中，a₁+a₅=10，a₄=7，则数列{a_n}的公差为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列命题中，真命题是（）

A、∃x₀∈R， $e^{x_{0}}$ ≤0 B、∀x∈R，2^x＞x² C、a+b=0的充要条件是 $\frac{a}{b}$ =﹣1 D、a＞1，b＞1是ab＞1的充分条件

查看试题解析
4. 一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（）

A、球 B、三棱锥 C、正方体 D、圆柱

查看试题解析
5. 下列不等式一定成立的是（）

A、lg（x²+ $\frac{1}{4}$ ）＞lgx（x＞0） B、sinx+ $\frac{1}{\sin x}$ ≥2（x≠kx，k∈Z） C、x²+1≥2|x|（x∈R） D、 $\frac{1}{x^{2} + 1} ＞ 1$ （x∈R）

查看试题解析
6. 如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{5}$ C、 $\frac{1}{6}$ D、 $\frac{1}{7}$

查看试题解析
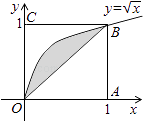7. 设函数 $D (x) = {\begin{matrix} 1, x 为有理数 \\ 0 ， x 为无理数 \end{matrix}$ ，则下列结论错误的是（）

A、D（x）的值域为{0，1} B、D（x）是偶函数 C、D（x）不是周期函数 D、D（x）不是单调函数

查看试题解析
8. 已知双曲线 $\frac{x^{2}}{4}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1的右焦点与抛物线y²=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于（）

A、 $\sqrt{5}$ B、 $4 \sqrt{2}$ C、3 D、5

查看试题解析
9. 若函数y=2^x图象上存在点（x，y）满足约束条件 ${\begin{matrix} x + y - 3 \leq 0 \\ x - 2 y - 3 \leq 0 \\ x \geq m \end{matrix}$ ，则实数m的最大值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
10. 函数f（x）在[a，b]上有定义，若对任意x₁ ， x₂∈[a，b]，有 $f (\frac{x_{1} + x_{2}}{2}) \leq \frac{1}{2} [f (x_{1}) + f (x_{2})]$ 则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
①f（x）在[1，3]上的图象是连续不断的；
②f（x²）在[1， $\sqrt{3}$ ]上具有性质P；
③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
④对任意x₁ ， x₂ ， x₃ ， x₄∈[1，3]，有 $f (\frac{x_{1} + x_{2} + x_{3} + x_{4}}{4}) \leq \frac{1}{4}$ [f（x₁）+f（x₂）+f（x₃）+f（x₄）]
其中真命题的序号是（）

A、①② B、①③ C、②④ D、③④

查看试题解析

二、填空题：把答案填在答题卡的相应位置．

11. （a+x）⁴的展开式中x³的系数等于8，则实数a=
．

查看试题解析
12. 阅读图所示的程序框图，运行相应地程序，输出的s值等于
．

查看试题解析
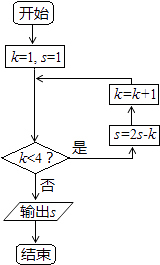13. 已知△ABC得三边长成公比为 $\sqrt{2}$ 的等比数列，则其最大角的余弦值为

查看试题解析
14. 数列{a_n}的通项公式a_n=ncos $\frac{n π}{2}$ +1，前n项和为S_n ，则S₂₀₁₂=

查看试题解析
15. 对于实数a和b，定义运算“*”：a*b= ${\begin{matrix} a^{2} - a b ， a \leq b \\ b^{2} - a b ， a > b \end{matrix}$ 设f（x）=（2x﹣1）*（x﹣1），且关于x的方程为f（x）=m（m∈R）恰有三个互不相等的实数根x₁ ， x₂ ， x₃ ，则x₁x₂x₃的取值范围是．

查看试题解析

三、解答题，解答题写出文字说明，证明过程或演算步骤．

16. 受轿车在保修期内维修费等因素的影响，企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年，现从该厂已售出的两种品牌轿车中随机抽取50辆，统计数据如下：
品牌
甲
乙
首次出现故障时间x（年）
0＜x＜1
1＜x≤2
x＞2
0＜x≤2
x＞2
轿车数量（辆）
2
3
45
5
45
每辆利润（万元）
1
2
3
1.8
2.9
将频率视为概率，解答下列问题：
（Ⅰ）从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为X₁ ，生产一辆乙品牌轿车的利润为X₂ ，分别求X₁ ， X₂的分布列；
（Ⅲ）该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌轿车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由．

查看试题解析
17. 某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．
1）sin²13°+cos²17°﹣sin13°cos17°
2）sin²15°+cos²15°﹣sin15°cos15°
3）sin²18°+cos²12°﹣sin18°cos12°
4）sin²（﹣18°）+cos²48°﹣sin²（﹣18°）cos48°
5）sin²（﹣25°）+cos²55°﹣sin²（﹣25°）cos55°
（Ⅰ）试从上述五个式子中选择一个，求出这个常数；
（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．

查看试题解析
18.
如图，在长方体ABCD﹣A₁B₁C₁D₁中AA₁=AD=1，E为CD中点．
（Ⅰ）求证：B₁E⊥AD₁；
（Ⅱ）在棱AA₁上是否存在一点P，使得DP∥平面B₁AE？若存在，求AP的长；若不存在，说明理由．
（Ⅲ）若二面角A﹣B₁E﹣A₁的大小为30°，求AB的长．

查看试题解析
19. 如图，椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为F₁ ，右焦点为F₂ ，离心率e= $\frac{1}{2}$ ．过F₁的直线交椭圆于A、B两点，且△ABF₂的周长为8．
（Ⅰ）求椭圆E的方程．
（Ⅱ）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．

查看试题解析
20. 已知函数f（x）=e^x+ax²﹣ex，a∈R．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求函数f（x）的单调区间；
（Ⅱ）试确定a的取值范围，使得曲线y=f（x）上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．

查看试题解析

四、选考题

21. （1）选修4﹣2：矩阵与变换
设曲线2x²+2xy+y²=1在矩阵A= $(\begin{matrix} a & 0 \\ b & 1 \end{matrix})$ （a＞0）对应的变换作用下得到的曲线为x²+y²=1．
（Ⅰ）求实数a，b的值．
（Ⅱ）求A²的逆矩阵．

查看试题解析
22. 选修4﹣4：坐标系与参数方程
在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为（2，0），（ $\frac{2 \sqrt{3}}{3} ， \frac{π}{2}$ ），圆C的参数方程 ${\begin{matrix} x = 2 + 2 \cos θ \\ y = - \sqrt{3} + 2 \sin θ \end{matrix}$ （θ为参数）．
（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；
（Ⅱ）判断直线l与圆C的位置关系．

查看试题解析
23. 已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]．
（Ⅰ）求m的值；
（Ⅱ）若a，b，c∈R，且 $\frac{1}{a} + \frac{1}{2 b} + \frac{1}{3 c}$ =m，求证：a+2b+3c≥9．

查看试题解析

品牌	甲			乙
首次出现故障时间x（年）	0＜x＜1	1＜x≤2	x＞2	0＜x≤2	x＞2
轿车数量（辆）	2	3	45	5	45
每辆利润（万元）	1	2	3	1.8	2.9