2015-2016学年湖南省衡阳四中高二下学期期中数学试卷

试卷更新日期：2016-09-18 类型：期中考试

进入出卷网下载

一、选择题

1. 设集合A={﹣2，﹣1，3，4}，B={﹣1，0，3}，则A∪B等于（　　）

A、{﹣1，3} B、{﹣2，﹣1，0，3，4} C、{﹣2，﹣1，0，4} D、{﹣2，﹣1，3，4}

查看试题解析
2. 某几何体的三视图都是全等图形，则该几何体一定是（）

A、球体 B、长方体 C、三棱锥 D、圆锥

查看试题解析
3. 函数 $f (x) = {(\frac{1}{2})}^{x} - x + 2$ 的零点所在的一个区间是（）

A、（﹣1，0） B、（0，1） C、（1，2） D、（2，3）

查看试题解析
4. 已知f（x）= ${\begin{matrix} 2^{x} (x \leq 0) \\ \log_{2} x (x > 0) \end{matrix}$ ，则f（4）=（）

A、1 B、2 C、3 D、4

查看试题解析
5. 执行如图所示的程序框图，若输出的S为4，则输入的x应为（）

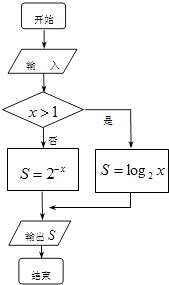A、﹣2 B、16 C、﹣2或8 D、﹣2或16

查看试题解析
6. 要完成下列两项调查：
（1）某社区有100户高收入家庭，210户中等收入家庭，90户低收入家庭，从中抽取100户调查消费购买力的某项指标；
（2）从某中学高二年级的10名体育特长生中抽取3人调查学习负担情况．
应采取的抽样方法是（）

A、（1）用系统抽样法，（2）用简单随机抽样法 B、（1）用分层抽样法，（2）用系统抽样法 C、（1）用分层抽样法，（2）用简单随机抽样法 D、（1）（2）都用分层抽样法

查看试题解析
7. 已知等比数列{a_n}的公比为2，则 $\frac{a_{4}}{a_{2}}$ 值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、2 D、4

查看试题解析
8. 一个袋中装有2个红球和2个白球，现从袋中取出1球，然后放回袋中再取出一球，则取出的两个球同色的概率为（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{5}$

查看试题解析
9. 函数f（x）= $\frac{1}{2}$ ﹣cos²（ $\frac{π}{4}$ ﹣x）的单调增区间是（）

A、[2kπ﹣ $\frac{π}{2}$ ，2kπ+ $\frac{π}{2}$ ]，k∈Z B、[2kπ+ $\frac{π}{2}$ ，2kπ+ $\frac{3 π}{4}$ ]，k∈Z C、[kπ+ $\frac{π}{4}$ ，kπ+ $\frac{3 π}{4}$ ]，k∈Z D、[kπ﹣ $\frac{π}{4}$ ，kπ+ $\frac{π}{4}$ ]，k∈Z

查看试题解析
10. 设a＞1，b＞2，且ab=2a+b，则a+b的最小值为（）

A、2 $\sqrt{2}$ B、2 $\sqrt{2}$ +1 C、2 $\sqrt{2}$ +2 D、2 $\sqrt{2}$ +3

查看试题解析

二、填空题

11. 在如图所示的茎叶图中，甲、乙两组数据的中位数分别是．

查看试题解析
12. 已知向量 $\vec{a}$ =（ $\sqrt{3}$ ，1）， $\vec{b}$ =（m，1）．若向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ ，则实数m= ．

查看试题解析
13. 过点A（2，3）且垂直于直线2x+y﹣5=0的直线方程为．

查看试题解析
14. 在△ABC中，|AB|=4，|AC|=2，∠A=60°，|BC|= ．

查看试题解析
15. 将正整数排成如图所示：其中第i行，第j列的那个数记为a_i^j ，则数表中的2015应记为．

查看试题解析

三、解答题

16. 已知sinα=﹣ $\frac{3}{5}$ ，α∈（﹣ $\frac{π}{2}$ ， $\frac{π}{2}$ ）．

(1)、求sin2α的值；

(2)、求tan（ $\frac{3 π}{4}$ ﹣α）的值．

查看试题解析
17. 设S_n为数列{a_n}的前n项和，且S_n=n²+n+1，n∈N^* ．

(1)、求数列{a_n}的通项公式；

(2)、求数列{ $\frac{1}{a_{n} a_{n + 1}}$ }的前n项和T_n ．

查看试题解析
18. 如图，在三棱锥P﹣ABC中，PA=PC=5，PB=4，AB=BC=2 $\sqrt{3}$ ，∠ACB=30°．

(1)、求证：AC⊥PB；

(2)、求三棱锥P﹣ABC的体积．

查看试题解析
19. 2013年第三季度，国家电网决定对城镇居民用电计费标准作出调整，并根据用电情况将居民分为三类：第一类的用电区间在（0，170]，第二类在（170，260]，第三类在（260，+∞）（单位：千瓦时）．某小区共有1000户居民，现对他们的用电情况进行调查，得到频率分布直方图，如图所示．

(1)、求该小区居民用电量的中位数与平均数；

(2)、本月份该小区没有第三类的用电户出现，为鼓励居民节约用电，供电部门决定：对第一类每户奖励20元钱，第二类每户奖励5元钱，求每户居民获得奖励的平均值；

(3)、利用分层抽样的方法从该小区内选出5位居民代表，若从该5户居民代表中任选两户居民，求这两户居民用电资费属于不同类型的概率．

查看试题解析
20. 在直角坐标系xOy中，圆C：x²+y²+4x﹣2y+m=0与直线x﹣ $\sqrt{3}$ y+ $\sqrt{3}$ ﹣2=0相切．

(1)、求圆C的方程；

(2)、若圆C上有两点M，N关于直线x+2y=0对称，且|MN|=2 $\sqrt{3}$ ，求直线MN的方程．

查看试题解析