备考2018年高考数学一轮基础复习：专题7 概率、随机变量及其分布

试卷更新日期：2017-11-28 类型：一轮复习

进入出卷网下载

一、单选题

1. A、B、C、D、E五个人参加抽奖活动，现有5个红包，每人各摸一个，5个红包中有2个8元，1个18元，1个28元，1个0元，（红包中金额相同视为相同红包），则A、B两人都获奖（0元视为不获奖）的情况有（）

A、18种 B、24种 C、36种 D、48种

查看试题解析
2. 已知X的分布列为
X
﹣1
0
1
P
   $\frac{1}{2}$
   $\frac{1}{3}$
   $\frac{1}{6}$
设y=2x+3，则E（Y）的值为（   ）

A、 $\frac{7}{3}$ B、4 C、﹣1 D、1

查看试题解析
3. 设点（a，b）是区域 ${\begin{matrix} x + y - 4 \leq 0 \\ x > 0 \\ y > 0 \end{matrix}$ 内的任意一点，则使函数f（x）=ax²﹣2bx+3在区间[ $\frac{1}{2}$ ，+∞）上是增函数的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
4. 将三颗骰子各掷一次，记事件A=“三个点数都不同”，B=“至少出现一个6点”，则条件概率P（A|B），P（B|A）分别是（）

A、 $\frac{60}{91}$ ， $\frac{1}{2}$ B、 $\frac{1}{2}$ ， $\frac{60}{91}$ C、 $\frac{5}{18}$ ， $\frac{60}{91}$ D、 $\frac{91}{216}$ ， $\frac{1}{2}$

查看试题解析
5. 已知某批零件的长度误差（单位：毫米）服从正态分布N（0，3²），从中随机取一件，其长度误差落在（3，6）内的概率为（）
附：若随机变量ξ服从正态分布N（μ，σ²），则P（μ﹣σ＜ξ＜μ+σ）=0.6826，P（μ﹣2σ＜ξ＜μ+2σ）=0.9544．

A、0.2718 B、0.0456 C、0.3174 D、0.1359

查看试题解析
6. 在如图的程序框图中，任意输入一次x（0≤x≤1）与y（0≤y≤1），则能输出“恭喜中奖！”的概率为（）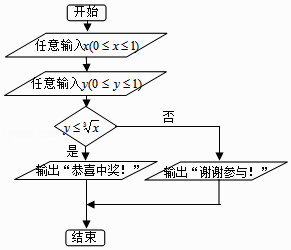

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
7. 在三棱锥的六条棱中任意选择两条，则这两条棱是一对异面直线的概率为（）

A、 $\frac{1}{20}$ B、 $\frac{1}{15}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
8. 已知随机变量η=8﹣ξ，若ξ～B（10，0.6），则Eη，Dη分别是（）

A、6和2.4 B、2和5.6 C、6和5.6 D、2和2.4

查看试题解析
9. 若实数x，y满足的约束条件 ${\begin{cases} x + y - 1 \leq 0 \\ x - y + 1 \geq 0 \\ y + 1 \geq 0 \end{cases}$ ，将一颗骰子投掷两次得到的点数分别为a，b，则函数z=2ax+by在点（2，﹣1）处取得最大值的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{6}$ D、 $\frac{5}{6}$

查看试题解析
10. 某地市高三理科学生有15000名，在一次调研测试中，数学成绩ξ服从正态分布N（100，σ²），已知p（80＜ξ≤100）=0.35，若按成绩分层抽样的方式取100份试卷进行分析，则应从120分以上的试卷中抽取（）

A、5份 B、10份 C、15份 D、20份

查看试题解析
11. 袋中装有大小相同的四个球，四个球上分别标有数字“2”，“3”，“4”，“6”.现从中随机选取三个球，则所选的三个球上的数字能构成等差数列的概率是（）

A、 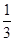$\frac{1}{4}$ B、 C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
12. 通讯中常采取重复发送信号的办法来减少在接收中可能发生的错误，假定接收一个信号时发生错误的概率是 $\frac{1}{10}$ ，为减少错误，采取每一个信号连发3次，接收时以“少数服从多数”的原则判断，则判错一个信号的概率为（）

A、 $\frac{1}{100}$ B、 $\frac{7}{250}$ C、 $\frac{1}{250}$ D、 $\frac{1}{1000}$

查看试题解析

二、填空题

13. 王先生家住 A 小区，他工作在 B 科技园区，从家开车到公司上班路上有 L₁ ， L₂两条路线（如图），L₁路线上有 A₁ ， A₂ ， A₃三个路口，各路口遇到红灯的概率均为 $\frac{1}{2}$ ；L₂路线上有 B₁ ， B₂两个路．各路口遇到红灯的概率依次为 $\frac{3}{4}$ ， $\frac{3}{5}$ ．若走 L₁路线，王先生最多遇到 1 次红灯的概率为；若走 L₂路线，王先生遇到红灯次数 X 的数学期望为．

查看试题解析
14. 商场经营的某种袋装大米质量（单位：kg）服从正态分布N（10，0.1²），任取一袋大米，质量不足9.8kg的概率为．（精确到0.0001）注：P（μ﹣σ＜x≤μ+σ）=0.6826，P（μ﹣2σ＜x≤μ+2σ）=0.9544，P（μ﹣3σ＜x≤μ+3σ）=0.9974．

查看试题解析
15. 同时抛掷5枚均匀的硬币160次，设5枚硬币正好出现1枚正面向上，4枚反面向上的次数为ξ，则ξ的数学期望是．

查看试题解析
16. 如图的矩形，长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，则我们可以估计出阴影部分的面积为．

查看试题解析

三、综合题

17. 某地区拟建立一个艺术搏物馆，采取竞标的方式从多家建筑公司选取一家建筑公司，经过层层筛选，甲、乙两家建筑公司进入最后的招标．现从建筑设计院聘请专家设计了一个招标方案：两家公司从6个招标总是中随机抽取3个总题，已知这6个招标问题中，甲公司可正确回答其中4道题目，而乙公司能正面回答每道题目的概率均为 $\frac{2}{3}$ ，甲、乙两家公司对每题的回答都是相独立，互不影响的．

(1)、求甲、乙两家公司共答对2道题目的概率；

(2)、请从期望和方差的角度分析，甲、乙两家哪家公司竞标成功的可能性更大？

查看试题解析

18. 为研究男女同学空间想象能力的差异，孙老师从高一年级随机选取了20名男生、20名女生，进行空间图形识别测试，得到成绩茎叶图如下，假定成绩大于等于80分的同学为“空间想象能力突出”，低于80分的同学为“空间想象能力正常”．

(1)、完成下面2×2列联表，

	空间想象能力突出	空间想象能力正常	合计
男生	$\underline{}$	$\underline{}$	$\underline{}$
女生	$\underline{}$	$\underline{}$	$\underline{}$
合计	$\underline{}$	$\underline{}$	$\underline{}$

(2)、判断是否有90%的把握认为“空间想象能力突出”与性别有关；

(3)、从“空间想象能力突出”的同学中随机选取男生2名、女生2名，记其中成绩超过90分的人数为ξ，求随机变量ξ的分布列和数学期望．

下面公式及临界值表仅供参考： $X^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

P（X²≥k）	0.100	0.050	0.010
k	2.706	3.841	6.635

查看试题解析

19. 大学开设甲、乙、丙三门选修课供学生任意选修（也可不选），假设学生是否选修哪门课彼此互不影响．已知某学生只选修甲一门课的概率为0.08，选修甲和乙两门课的概率为0.12，至少选修一门的概率是0.88．

(1)、求该学生选修甲、乙、丙的概率分别是多少？

(2)、用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积，求ξ的分布列和数学期望．

查看试题解析
20. 某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：

(1)、记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；

(2)、若购进这批小龙虾100千克，试估计这批小龙虾的数量；

(3)、为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
等级
一等品
二等品
三等品
重量（g）
[5，25）
[25，45）
[45，55]
按分层抽样抽取10只，再随机抽取3只品尝，记X为抽到二等品的数量，求抽到二级品的期望．

查看试题解析
21. 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．

(1)、若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n∈N）的函数解析式．

(2)、花店记录了100天玫瑰花的日需求量（单位：枝），整理得如表：
日需求量n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率．
（i）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由．

查看试题解析
22. 甲、乙两人各射击一次，击中目标的概率分别是 $\frac{2}{3}$ 和 $\frac{3}{4}$ ．假设两人射击是否击中目标，相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响．

(1)、求甲射击4次，至少1次未击中目标的概率；

(2)、求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；

(3)、假设某人连续2次未击中目标，则停止射击．问：乙恰好射击5次后，被中止射击的概率是多少？

查看试题解析

等级	一等品	二等品	三等品
重量（g）	[5，25）	[25，45）	[45，55]

X	﹣1	0	1
P	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{6}$

日需求量n	14	15	16	17	18	19	20
频数	10	20	16	16	15	13	10