浙江省宁波市北仑区2017年中考数学模拟试卷
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题
-
1. 下列实数中最大的是( )A、 B、0 C、( )﹣1 D、|﹣ |2. 下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1094. 下列计算正确的是( )A、3x4﹣x2=3x2 B、(﹣2ab3)2•a=4a3b6 C、8a6÷2a3=4a2 D、(a﹣2)2=a2﹣45. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
3. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1094. 下列计算正确的是( )A、3x4﹣x2=3x2 B、(﹣2ab3)2•a=4a3b6 C、8a6÷2a3=4a2 D、(a﹣2)2=a2﹣45. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )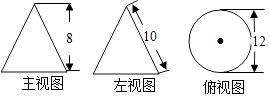 A、40π B、48π C、60π D、80π6. 为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果绘制成了如图所示的条形统计图,则这组数据的众数和中位数分别是( )
A、40π B、48π C、60π D、80π6. 为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果绘制成了如图所示的条形统计图,则这组数据的众数和中位数分别是( )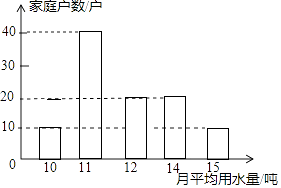 A、40,20 B、11,11 C、11,12 D、11,11.57. 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
A、40,20 B、11,11 C、11,12 D、11,11.57. 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )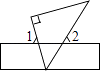 A、108° B、72° C、77° D、82°8. 已知不等式组 的最小整数解为a,最大整数解为b,则ba=( )
A、108° B、72° C、77° D、82°8. 已知不等式组 的最小整数解为a,最大整数解为b,则ba=( )
A、 B、﹣8 C、 D、169. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )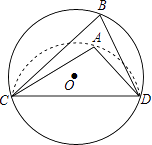 A、110° B、70° C、60° D、55°10. 设M(m,n)在反比例函数y=﹣ 上,其中m是分式方程 ﹣1= 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A、110° B、70° C、60° D、55°10. 设M(m,n)在反比例函数y=﹣ 上,其中m是分式方程 ﹣1= 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A、y=﹣ x﹣ B、y= x+ C、y=4x﹣5 D、y=﹣4x+511. 如图,已知矩形ABCD满足AB:BC=1: ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )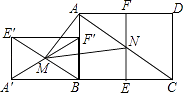 A、4 B、4 C、2 D、112. 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y= (x>0)的图象过点E.若△BCD的面积为2 ,则k的值为( )
A、4 B、4 C、2 D、112. 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y= (x>0)的图象过点E.若△BCD的面积为2 ,则k的值为( )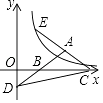 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2二、填空题
-
13. 函数y= 中,自变量x的取值范围是 .14. 分解因式:x3y﹣4xy= .15. 平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2= .
 16. 已知m是方程x2﹣2017x+1=0的一个根,则代数式m2﹣2018m+ +3的值是 .17. 若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(﹣1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为 .
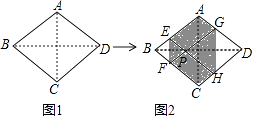
16. 已知m是方程x2﹣2017x+1=0的一个根,则代数式m2﹣2018m+ +3的值是 .17. 若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(﹣1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为 .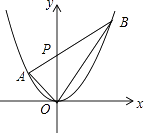 18. 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
18. 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是菱形ABCD的中心;
②当x= 时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)
三、解答题
-
19. 先化简,再求值:(a+3)(a﹣3)+a(1﹣a),其中a=10.
20. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: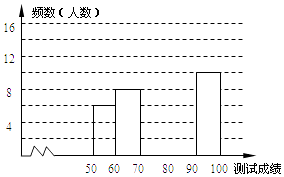
请结合图表完成下列各题:
(1)、①表中a的值为 , 中位数在第组;②频数分布直方图补充完整;
(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
21.
(1)、如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).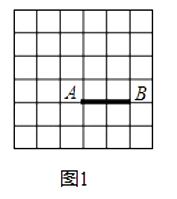 (2)、如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F= .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
(2)、如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F= .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.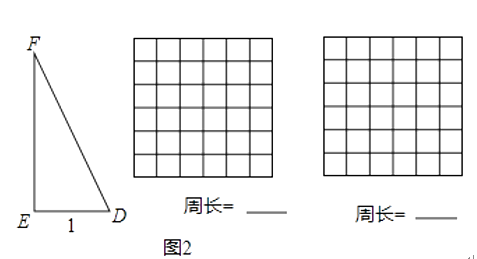 22. 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1= ,直线AC解析式为y2=ax+b.
22. 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1= ,直线AC解析式为y2=ax+b.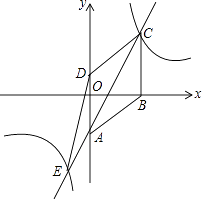 (1)、求反比例函数解析式;(2)、当y1<y2时,求x的取值范围;
(1)、求反比例函数解析式;(2)、当y1<y2时,求x的取值范围;
(3)、求△CDE的面积.
23. 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.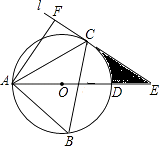 (1)、求证:AC平分∠FAD;(2)、已知AF=3 ,求阴影部分面积.24. 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)、求证:AC平分∠FAD;(2)、已知AF=3 ,求阴影部分面积.24. 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.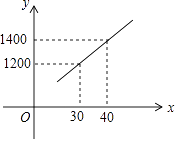 (1)、直接写出y2与x之间的函数关系式;
(1)、直接写出y2与x之间的函数关系式;
(2)、求月产量x的范围;
(3)、当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
25. 定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
(1)、根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;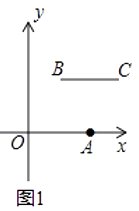
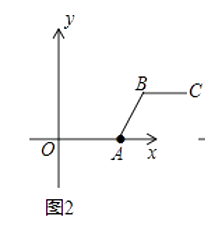 (2)、如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(2)、如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.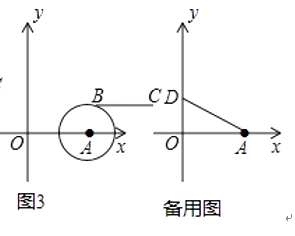 (3)、当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由.
(3)、当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由.
26. 已知抛物线C1:y=﹣ x2+bx+c的对称轴是x=2,且经过点(6,0).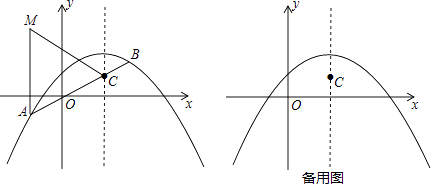 (1)、求抛物线C1的解析式;(2)、将抛物线C1向下平移2个单位后得到抛物线C2 , 如图,直线y=kx﹣2k+1交抛物线C2于A,B两点(点A在点B的左边),交抛物线C2的对称轴于点C,M(xA , 3),xA表示点A横坐标,求证:AC=AM;(3)、在(2)的条件下,请你参考(2)中的结论解决下列问题:
(1)、求抛物线C1的解析式;(2)、将抛物线C1向下平移2个单位后得到抛物线C2 , 如图,直线y=kx﹣2k+1交抛物线C2于A,B两点(点A在点B的左边),交抛物线C2的对称轴于点C,M(xA , 3),xA表示点A横坐标,求证:AC=AM;(3)、在(2)的条件下,请你参考(2)中的结论解决下列问题:①若CM=AM,求 的值;
②请你探究:在抛物线C2上是否存在点P,使得PO+PC取得最小值?如果存在,求出点P的坐标;如果不存在,请说明理由.