吉林省长春市朝阳区2017年中考数学模拟试卷(5月份)
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题
-
1. ﹣2017的相反数是( )A、2017 B、 C、﹣ D、02. 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为55000000千米,这个数据用科学记数法可表示为( )
A、5.5×106 B、5.5×107 C、55×106 D、0.55×1083. 如图是由五个完全相同的小正方体组成的几何体,若将最左边的小正方体拿掉,则下列结论正确的是( ) A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图不变4. 一元二次方程x2+2x+2=0根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、不能确定5. 如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( )
A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图不变4. 一元二次方程x2+2x+2=0根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、不能确定5. 如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( ) A、2 B、4 C、6 D、86. 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A,B,C,若∠BCO=45°,则∠BAC的大小为( )
A、2 B、4 C、6 D、86. 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A,B,C,若∠BCO=45°,则∠BAC的大小为( )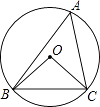 A、22.5° B、35° C、45° D、67.5°7. 如图,在平面直角坐标系中,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y= (x>0)在第一象限内的图象上,则k的值为( )
A、22.5° B、35° C、45° D、67.5°7. 如图,在平面直角坐标系中,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y= (x>0)在第一象限内的图象上,则k的值为( ) A、1 B、2 C、3 D、48. 如图,正方形ABCD的边长为2,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x.在下列图象中,能表示△ADP的面积y关于x的函数关系的图象是下列选项中的( )
A、1 B、2 C、3 D、48. 如图,正方形ABCD的边长为2,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x.在下列图象中,能表示△ADP的面积y关于x的函数关系的图象是下列选项中的( ) A、
A、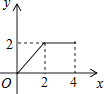 B、
B、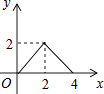 C、
C、 D、
D、
二、填空题
-
9. 计算6x3•x2的结果是 .10. 不等式3x﹣2>4的解是 .11. 如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A,B,C和点D,E,F.若AB=2,BC=4,则 的值为 .
 12. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为度.
12. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为度.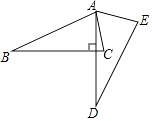 13. 如图,AB切⊙O于点B,BC∥OA,交⊙O于点C,若∠OAB=30°,BC=6,则劣弧BC的长为 .
13. 如图,AB切⊙O于点B,BC∥OA,交⊙O于点C,若∠OAB=30°,BC=6,则劣弧BC的长为 . 14. 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=﹣x2﹣5x+c经过点B、C,则菱形ABCD的面积为 .
14. 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=﹣x2﹣5x+c经过点B、C,则菱形ABCD的面积为 .
三、解答题
-
15. 先化简,再求值: + ,其中x= ﹣1.
16. 有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.17. 甲、乙两名学生练习计算机打字,甲打一篇1000字的文章与乙打一篇800字的文章所用的时间相同.已知甲每分钟比乙每分钟多打10个字.求甲、乙两人每分钟各打多少字?
18. 如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.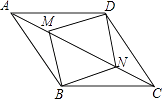 19. 如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)
19. 如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)【参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20】
 20. .雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅会影响人们的出行,还影响着人们的健康,但是人们到底对雾霾了解多少呢?带着这种思考,某学校九年级综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了本市部分市民的观点(分四类:A类工业污染;B类汽车尾气排放;C类燃煤问题;D类其他原因.调查的每名市民只选择一种类别),并对调查结果进行录入整理,绘制了如下两幅不完整的统计图.
20. .雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅会影响人们的出行,还影响着人们的健康,但是人们到底对雾霾了解多少呢?带着这种思考,某学校九年级综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了本市部分市民的观点(分四类:A类工业污染;B类汽车尾气排放;C类燃煤问题;D类其他原因.调查的每名市民只选择一种类别),并对调查结果进行录入整理,绘制了如下两幅不完整的统计图.
请根据图中提供的信息解答下列问题:
(1)、求出本次调查的市民人数,并补全条形统计图.(2)、估计该市800万名市民中持有A、B两类看法的总人数.(3)、结合本次调查结果,请你给出一条“为减少雾霾天气发生”的合理化的建议.21. 在一条直线上依次有A,B,C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示. (1)、A,C两港口间的距离为海里,a=
(1)、A,C两港口间的距离为海里,a=
(2)、求y与x之间的函数关系式.(3)、在B岛上有一个不间断发射信号的信号发射台,发射的信号覆盖半径为8海里的圆形区域,求该海巡船鞥接受到该信号的时间有多长?
22. 新定义:我们把只有一组对角是直角的四边形叫做准矩形.
(1)、图①、图②均为3×3的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC的端点均在格点上,在图①、图②中各画一个准矩形ABCD,要求:准矩形ABCD的顶点D在格点上,且两个准矩形不全等.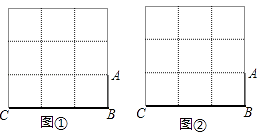 (2)、如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积
(2)、如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积 23. 如图,在矩形ABCD中,AB=3,AD=4,点P从点A出发,沿折线AC﹣CB向终点B运动,点P在AC上的速度为每秒2个单位长度,在CB上的速度为每秒1个单位长度,同时,点Q从点A出发,沿AC以每秒1个单位长度的速度向终点C运动,当点Q到达终点时,点P也随之停止.过点P作PM⊥AD于点M,连接QM,以PM、QM为邻边作▱PMQN,设▱PMQN与矩形ABCD重叠部分图形的周长为d(长度单位),点P的运动时间为t(秒)(t>0)
23. 如图,在矩形ABCD中,AB=3,AD=4,点P从点A出发,沿折线AC﹣CB向终点B运动,点P在AC上的速度为每秒2个单位长度,在CB上的速度为每秒1个单位长度,同时,点Q从点A出发,沿AC以每秒1个单位长度的速度向终点C运动,当点Q到达终点时,点P也随之停止.过点P作PM⊥AD于点M,连接QM,以PM、QM为邻边作▱PMQN,设▱PMQN与矩形ABCD重叠部分图形的周长为d(长度单位),点P的运动时间为t(秒)(t>0) (1)、求AC的长(2)、用含t的代数式表示线段CP的长.(3)、当点P在线段AC上时,求d与t之间的函数关系式.(4)、经过点N的直线将矩形ABCD的面积平分,若该直线同时将▱PMQN的面积分成1:3的两部分,直接写出此时t的值.24. 如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0)、B(3,0).抛物线y=x2﹣2mx+m2﹣4的顶点为P,与y轴的交点为Q.
(1)、求AC的长(2)、用含t的代数式表示线段CP的长.(3)、当点P在线段AC上时,求d与t之间的函数关系式.(4)、经过点N的直线将矩形ABCD的面积平分,若该直线同时将▱PMQN的面积分成1:3的两部分,直接写出此时t的值.24. 如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0)、B(3,0).抛物线y=x2﹣2mx+m2﹣4的顶点为P,与y轴的交点为Q. (1)、填空:点P的坐标为;点Q的坐标为(均用含m的代数式表示)(2)、当抛物线经过点A时,求点Q的坐标.(3)、连接QA、QB,设△QAB的面积为S,当抛物线与线段AB有公共点时,求S与m之间的函数关系式.(4)、点P、Q不重合时,以PQ为边作正方形PQMN(P、Q、M、N分别按顺时针方向排列).当正方形PQMN的四个顶点中,位于x轴两侧或y轴两侧的顶点个数相同时,直接写出此时m的取值范围.
(1)、填空:点P的坐标为;点Q的坐标为(均用含m的代数式表示)(2)、当抛物线经过点A时,求点Q的坐标.(3)、连接QA、QB,设△QAB的面积为S,当抛物线与线段AB有公共点时,求S与m之间的函数关系式.(4)、点P、Q不重合时,以PQ为边作正方形PQMN(P、Q、M、N分别按顺时针方向排列).当正方形PQMN的四个顶点中,位于x轴两侧或y轴两侧的顶点个数相同时,直接写出此时m的取值范围.