吉林省长春六十八中2017年中考数学二模试卷
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题
-
1. 的值是( )A、﹣4 B、4 C、﹣2 D、22. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x>2 B、x<2 C、x≠﹣2 D、x≠23. 下列计算结果是a8的值是( )A、a2•a4 B、a2+a6 C、(a2)4 D、a9﹣a4. “一次抛六枚均匀的骰子,朝上一面的点数都为6”这一事件是( )A、必然事件 B、随机事件 C、确定事件 D、不可能事件5. 运用乘法公式计算(m﹣2)2的结果是( )A、m2﹣4 B、m2﹣2m+4 C、m2﹣4m+4 D、m2+4m﹣46.
如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1 , 则a+b的值为( )
 A、2 B、3 C、4 D、57. 下图是几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,( )图是这个几何体的主视图.
A、2 B、3 C、4 D、57. 下图是几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,( )图是这个几何体的主视图.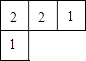 A、
A、 B、
B、 C、
C、 D、
D、 8. 五名学生投篮球,规定每人投20次,统计他们每人投中的次数.得到五个数据.若这五个数据的中位数是6.唯一众数是7,则他们投中次数的总和可能是( )
8. 五名学生投篮球,规定每人投20次,统计他们每人投中的次数.得到五个数据.若这五个数据的中位数是6.唯一众数是7,则他们投中次数的总和可能是( )
A、20 B、28 C、30 D、319. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( ) A、84 B、336 C、510 D、132610. 二次函数y=ax2+bx+c(a≠0)和正比例函数y= x的图象如图所示,则方程ax2+(b﹣ )x+c=0(a≠0)的两根之和( )
A、84 B、336 C、510 D、132610. 二次函数y=ax2+bx+c(a≠0)和正比例函数y= x的图象如图所示,则方程ax2+(b﹣ )x+c=0(a≠0)的两根之和( )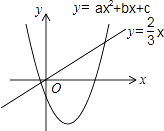 A、大于0 B、等于0 C、小于0 D、不能确定
A、大于0 B、等于0 C、小于0 D、不能确定二、填空题
-
11. 计算5﹣(﹣2)的结果为 .12. 化简: = .13. 在一个不透明的袋子里装有一个黑球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球,两次都摸到黑球的概率是 .14. 如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′= .
 15. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为 .
15. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为 .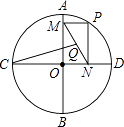 16. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .
16. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .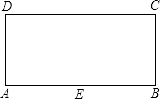
三、解答题
-
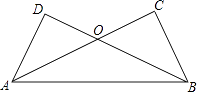
17. 解方程:15x﹣3=3(x﹣4)18. 如图,已知OC=OD,∠OAB=∠OBA,求证:AD=BC.
 19. 某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
19. 某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下: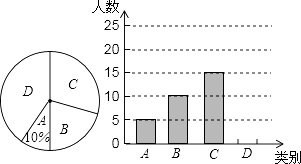
请结合图中信息解答下列问题:
(1)、九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;(2)、请将条形统计图补充完整;(3)、若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?20. 某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)、若工厂计划获利14万元,问A,B两种产品应分别生产多少件?(2)、若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?21. 如图AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.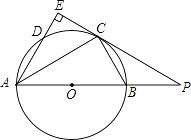 (1)、探究线段PB,AB之间的数量关系,并说明理由;
(1)、探究线段PB,AB之间的数量关系,并说明理由;
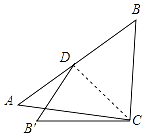
(2)、若AD=3,求AB长.22. 在四边形ABCD中,AB=AD,BC=CD.(1)、如图1,请连接AC,BD,求证:AC垂直平分BD;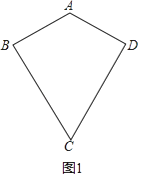 (2)、如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(2)、如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;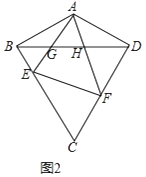 (3)、如图3,在(2)的条件下,若 EF⊥CD,直接写出 的值.
(3)、如图3,在(2)的条件下,若 EF⊥CD,直接写出 的值.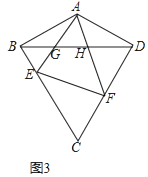 23. 已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ).(1)、求tan∠OPQ的值;(2)、将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
23. 已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ).(1)、求tan∠OPQ的值;(2)、将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.