湖南省长沙二十九中2017年中考数学模拟试卷
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题:
-
1. 一袋大米的标准重量为10kg.把一袋重10.5kg的大米记为+0.5kg,则一袋重9.8kg的大米记为( )A、﹣9.8kg B、+9.8kg C、﹣0.2kg D、0.2kg2. 下列各组中运算结果相等的是( )A、23与32 B、(﹣2)4与﹣24 C、(﹣2)3与﹣23 D、 与3. 下列各式计算正确的是( )A、2a2+3a2=5a4 B、(﹣2ab)3=﹣6ab3 C、(3a+b)(3a﹣b)=9a2﹣b2 D、a3•(﹣2a)=﹣2a34. 下列四个图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 已知5名学生的体重分别是41、50、53、49、67(单位:kg),则这组数据的极差是( )A、8 B、9 C、26 D、416. 将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )
5. 已知5名学生的体重分别是41、50、53、49、67(单位:kg),则这组数据的极差是( )A、8 B、9 C、26 D、416. 将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )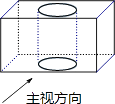 A、
A、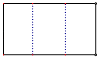 B、
B、 C、
C、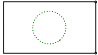 D、
D、 7. 若函数y=(k+1)x+k2﹣1是正比例函数,则k的值为( )A、0 B、1 C、±1 D、﹣18. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
7. 若函数y=(k+1)x+k2﹣1是正比例函数,则k的值为( )A、0 B、1 C、±1 D、﹣18. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) A、①② B、①②③ C、①②④ D、①②③④
A、①② B、①②③ C、①②④ D、①②③④二、填空题:
-
9. 的平方根是 .10. 分解因式:x2﹣4(x﹣1)= .11. 函数 中.自变量x的取值范围是 .12. 如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是 .
 13. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
13. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
318
652
793
1604
4005
发芽频率
0.850
0.795
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.10).
14. 如图,要使△ABC∽△ACD,需补充的条件是 . (只要写出一种) 15. 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是 .
15. 为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是 . 16. 计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳计算结果中的个位数字的规律,猜测32015﹣1的个位数字是 .
16. 计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳计算结果中的个位数字的规律,猜测32015﹣1的个位数字是 .
三、解答题:
-
17. 计算: ﹣(π﹣2016)0+| ﹣2|+2sin60°.18.
解不等式组 请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得
(Ⅱ)解不等式②,得
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为
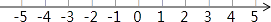 19. 已知反比例函数y= 的图象经过点M(2,1)(1)、求该函数的表达式;(2)、当2<x<4时,求y的取值范围(直接写出结果).20. 把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.21. 某商品交易会上,一商人将每件进价为5元的纪念品,按每件9元出售,每天可售出32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价2元,每天的销售量会减少8件.
19. 已知反比例函数y= 的图象经过点M(2,1)(1)、求该函数的表达式;(2)、当2<x<4时,求y的取值范围(直接写出结果).20. 把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.21. 某商品交易会上,一商人将每件进价为5元的纪念品,按每件9元出售,每天可售出32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价2元,每天的销售量会减少8件.
(1)、当售价定为多少元时,每天的利润为140元?(2)、写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价﹣进价)×售出件数)22. 如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 23. 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;
23. 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;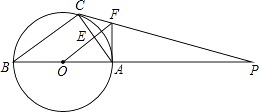 (1)、判断AF与⊙O的位置关系并说明理由.(2)、若⊙O的半径为4,AF=3,求AC的长.24. 某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)、判断AF与⊙O的位置关系并说明理由.(2)、若⊙O的半径为4,AF=3,求AC的长.24. 某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)、求第一批购进书包的单价是多少元?(2)、若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?四、综合题:
-
25. 在平面直角坐标系中,已知A,B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限.(1)、如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A,B两点的横坐标的乘积;
 (2)、如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,求证:A、B两点横坐标的乘积是一个定值;
(2)、如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,求证:A、B两点横坐标的乘积是一个定值; (3)、在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为 .那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(3)、在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为 .那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
26. 在正方形ABCD中,连接BD.
(1)、如图1,AE⊥BD于E.直接写出∠BAE的度数. (2)、如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.
(2)、如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)、如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)