黑龙江省哈尔滨六十九中2017年中考数学模拟试卷
试卷更新日期：2017-11-27 类型：中考模拟
一、选择题
-
1. 下列实数中，无理数是（ ）A、﹣ B、 C、 D、﹣|﹣5|2. 下列运算正确的是（ ）A、m4•m2=m8 B、（m2）3=m6 C、3m﹣2m=2 D、（m﹣n）2=m2﹣n23. 下列图形中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
4. 如图，是一个由3个相同的正方体组成的立体图形，则它的主视图为（ ）
A、
B、
C、
D、
5. 不等式组 的解集是（ ）A、﹣1＜x≤3 B、﹣1＜x＜3 C、x＞﹣1 D、x≤36. 已知反比例函数y= 的图象位于第一、第三象限，则k的取值范围是（ ）A、k＞2 B、k≥2 C、k≤2 D、k＜27. 如图、将△ABC绕着点C按顺时针方向旋转20°，B点落在B′位置，点A落在A′位置．若A′C⊥AB，则∠B′A′C的度数是（ ）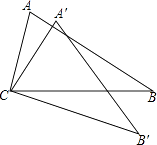
A、50° B、60° C、70° D、80°8. 在△ABC中，∠C=90°，BC=2，sinA= ，则边AC的长是（ ）A、 B、3 C、 D、9. 如图，在平行四边形ABCD中，EF∥AB，DE：AE=2：3，△BDC的面积为25，则四边形AEFB的面积为（ ）
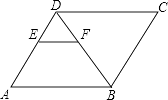A、25 B、9 C、21 D、1610. 如图，小磊老师从甲地去往10千米的乙地，开始以一定的速度行驶，之后由于道路维修，速度变为原来的四分之一，过了维修道路后又变为原来的速度到达乙地．设小磊老师行驶的时间为x（分钟），行驶的路程为y（千米），图中的折线表示y与x之间的函数关系，则小磊老师从甲地到达乙地所用的时间是（ ）
A、15分钟 B、20分钟 C、25分钟 D、30分钟二、填空题
-
11. 数6260000用科学记数法可表示为 ．12. 函数y= 中自变量x的取值范围是 ．13. 因式分解：ax2﹣4axy+4ay2= ．14. 计算： ÷ = ．
15. 某种衬衫每件的标价为150元，如果每件以8折（即按标价的80%）出售，那么这种衬衫每件的实际售价应为元．16. 分别写有﹣5，﹣9，0，5，9的五张外观形状完全相同的卡片，蒙上眼睛从中任抽一张，那么抽到表示非负数的卡片概率是 ．
17. 已知扇形的圆心角为120°，半径为6，则扇形面积是 ．18. 如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC+BD=24cm，△OAB的周长是18cm，则EF=cm．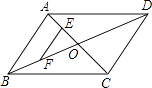
19. 用直角边分别为3和4的两个直角三角形拼成一个平行四边形（非矩形），所得的平行四边形的周长是 ．
20. 已知矩形ABCD，点E在AD边上，DE＞AE，连接BE，将△ABE沿着BE翻折得到△BFE，射线EF交BC于G，若点G为BC的中点，FG=1，DE=6，则AE的长 ．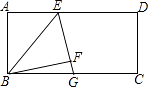
三、解答题
-
21. 先化简，再求值： ÷（1﹣ ），其中x= sin45°+2tan60°．22. 图1、图2分别是7×6的网格，网格中的每个小正方形的边长均为1，点A、B在小正方形的顶点上．
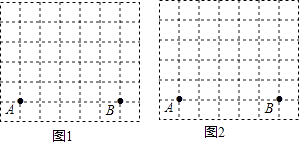(1)、在图1中确定点C（点C在小正方形的顶点上），要求以A、B、C为顶点的三角形为锐角等腰三角形，画出此三角形（画出一个即可）；(2)、在图2中确定点D（点D在小正方形的顶点上），要求以A、B、D为顶点的三角形是以AB为斜边的直角三角形，画出此三角形（画出一个即可），并直接写出此三角形的周长
23. 为评估九年级学生的学习成绩状况，以应对即将到来的中考做好教学调整，某中学抽取了部分参加考试的学生的成绩作为样本分析，绘制成了如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：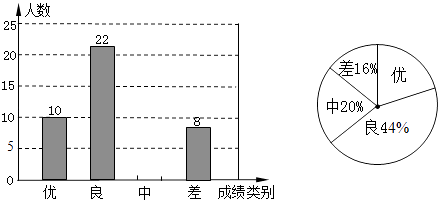
(1)、求本中学成绩类别为“中”的人数；
(2)、求出扇形图中，“优”所占的百分比，并将条形统计图补充完整；
(3)、该校九年级共有1000人参加了这次考试，请估算该校九年级共有多少名学生的数学成绩达到优秀？
24. 已知：如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．
(1)、求证：BE=DG；(2)、已知tanB= ，AB=5，若四边形ABFG是菱形，求平行四边形ABCD的面积．
25. 某文教店用1200元购进了甲、乙两种钢笔．已知甲种钢笔进价为每支12元，乙种钢笔进价为每支10元．文教店在销售时甲种钢笔售价为每支15元，乙种钢笔售价为每支12元，全部售完后共获利270元．
(1)、求这个文教店购进甲、乙两种钢笔各多少支？(2)、若该文教店以原进价再次购进甲、乙两种钢笔，且购进甲种钢笔的数量不变，而购进乙种钢笔的数量是第一次的2倍，乙种钢笔按原售价销售，而甲种钢笔降价销售．当两种钢笔销售完毕时，要使再次购进的钢笔获利不少于340元，甲种钢笔最低售价每支应为多少元？26. 已知AB为⊙O的直径，BM为⊙O的切线，点C为射线BM上一点，连接AC交⊙O于点D，点E为BC上一点．连接AE交半圆于F．
(1)、如图1，若AE平分∠BAC，求证：∠DBF=∠CBF；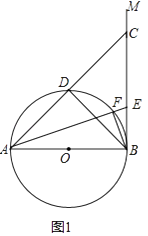
(2)、如图2，过点D作⊙O的切线交BM于N，若DN⊥BM，求证：△ABC为等腰直角三角形；
(3)、在（2）的条件下，如图3，延长BF交AC于G，点H为AB上一点，且BH=2BE，过点H作AE的垂线交AC于P，连接OG交DN于K，若AP=CG，EF=1，求GK的长．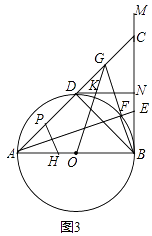
27. 如图，已知抛物线y=﹣x2+bx+c与x轴交于A，B与y轴交于C，过C作x轴的平行线交抛物线于点D，过点D作x轴的垂线交x轴于E，点D的坐标为（2，3）
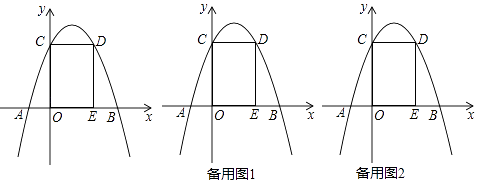(1)、求抛物线的解析式；(2)、点P为第一象限直线DE右侧抛物线上一点，连接AP交y轴于点F，连接PD、DF，设点P的横坐标为t，△PFD的面积为S，求S与t的函数关系式；
(3)、在（2）的条件下，点P向下平移3个单位得到点Q，连接AQ、EQ，若∠AQE=45°，求点P的横坐标．