黑龙江省哈尔滨二十六中2017年中考数学模拟试卷(4月份)
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题:
-
1. 2017的绝对值是( )A、﹣2017 B、2017 C、 D、﹣2. 下列运算正确的是( )A、(ab)2=ab2 B、3a+2a2=5a2 C、 =﹣4 D、a•a=a23. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
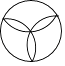 B、
B、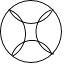 C、
C、 D、
D、 4. 由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )
4. 由6个完全相同的小正方体组成的立体图形如图所示,则在以下视图中,与其它三个形状都不同的是( )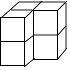 A、主视图 B、俯视图 C、左视图 D、右视图5. 2017年某市中考体育考试包括必考和选考两项.必考项目:男生1000米跑;女生800米跑;选考项目(五项中任选两项):A.掷实心球、B.篮球运球、C.足球运球、D.立定跳远、E.一分钟跳绳.那么小丽同学考“800米跑、立定跳远、一分钟跳绳”的概率是( )
A、主视图 B、俯视图 C、左视图 D、右视图5. 2017年某市中考体育考试包括必考和选考两项.必考项目:男生1000米跑;女生800米跑;选考项目(五项中任选两项):A.掷实心球、B.篮球运球、C.足球运球、D.立定跳远、E.一分钟跳绳.那么小丽同学考“800米跑、立定跳远、一分钟跳绳”的概率是( )
A、 B、 C、 D、6. 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )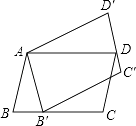 A、100° B、105° C、115° D、120°7. 如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A、100° B、105° C、115° D、120°7. 如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )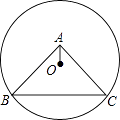 A、6 B、13 C、 D、28. 将函数y=﹣2x的图象向下平移3个单位后与y轴的交点坐标为( )A、(﹣3,0) B、( ,0) C、(0,3) D、(0,﹣3)9. 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
A、6 B、13 C、 D、28. 将函数y=﹣2x的图象向下平移3个单位后与y轴的交点坐标为( )A、(﹣3,0) B、( ,0) C、(0,3) D、(0,﹣3)9. 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )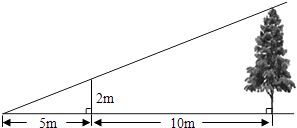 A、5m B、6m C、7m D、8m10. 一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.
A、5m B、6m C、7m D、8m10. 一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.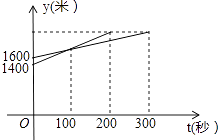 A、2000米 B、2100米 C、2200米 D、2400米
A、2000米 B、2100米 C、2200米 D、2400米二、填空题
-
11. 现在网购越来越多地成为人们的一种消费方式,在2016年的“双11”网上促销活动中天猫和淘宝的支付交易额突破120700000000元,将120700000000用科学记数法表示为 .12. 在函数y= 中,自变量x的取值范围是 .13. 分解因式:a3﹣4a2b+4ab2= .14. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为 .
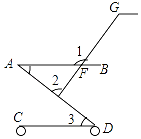 15. 反比例函数y= 的图象经过点(1,6)和(m+1,﹣3),则m= .
15. 反比例函数y= 的图象经过点(1,6)和(m+1,﹣3),则m= .
16. 不等式组 的最小整数解是 .17. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则 的长 .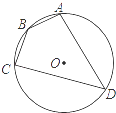 18. 如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
18. 如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .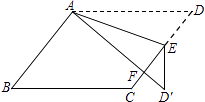 19. 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .
19. 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .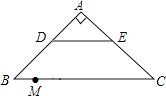 20. 如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ,BG=4,则GH的长为 .
20. 如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ,BG=4,则GH的长为 .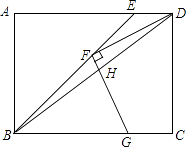
三、解答题
-
21. 先化简,再求值 • ﹣ ,其中x=tan45°+2sin45°,y= tan30°﹣2 cos60°.
22. 图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.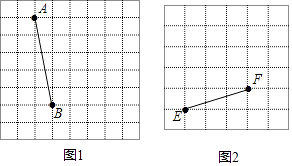 (1)、如图1,作出以AB为对角线的正方形并直接写出正方形的周长;(2)、如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4.
(1)、如图1,作出以AB为对角线的正方形并直接写出正方形的周长;(2)、如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4.
23. 为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况.小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.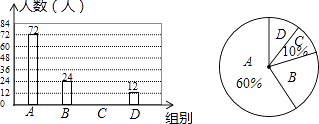
回答下列问题:
(1)、这次被抽查的学生共有人,扇形统计图中,“B组”所对应的圆心角的度数为;
(2)、补全条形统计图;(3)、已知该中学共有学生2500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
24. 如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G.求证: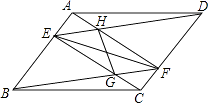 (1)、EF与GH互相平分;
(1)、EF与GH互相平分;
(2)、在不添加任何辅助线和字母的条件下,请直接写出图中所有的全等的三角形.
25. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
26. 在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)、如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;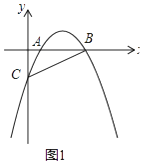 (2)、如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(2)、如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;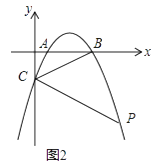 (3)、如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.
(3)、如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.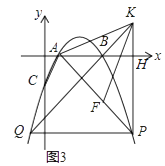 27. 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
27. 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.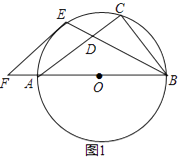
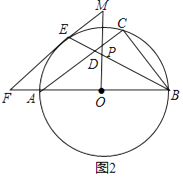
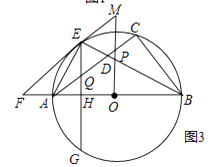
(1)、如图1,求证:EF∥AC;
(2)、如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)、如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ,EQ=5,求PM的值.