河南省郑州市2017年中考数学二模试卷
试卷更新日期：2017-11-27 类型：中考模拟
一、选择题
-
1. ﹣2017的绝对值是（ ）A、2017 B、﹣2017 C、 D、﹣2. 下列四个手机应用图标中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 随着信息技术的不断发展，微信已经成为人们生活中不可或缺的沟通工具，2017年2月，腾讯公司发不了《2017微信春节数据报告》，报告中显示，全国今年除夕至初五微信红包收发总量约46000000000个，把46000000000用科学记数法表示为（ ）A、4.6×109 B、4.6×1010 C、4.6×1011 D、46×1084. 如图，把含30°角的直角三角板的直角顶点C放在直线a上，其中∠A=30°，直角边AC和斜边AB分别与直线b相交，如果a∥b，且∠1=25°，则∠2的度数为（ ）
A、20° B、25° C、30° D、35°5. 某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表，根据表中的信息判断，下列结论中错误的是（ ）成绩（分）
30
29
28
26
18
人数（人）
32
4
2
1
1
A、该班共有40名学生 B、该班学生这次考试成绩的平均数为29.4分 C、该班学生这次考试成绩的众数为30分 D、该班学生这次考试成绩的中位数为28分6. 如图，两条直线分别被三条平行直线l1 ， l2 ， l3所截，若AB=3，BC=6，DE=2，则DF的长为（ ）
A、4 B、5 C、6 D、77. 某校九年级学生从学校出发，到相距8千米的科技馆参观，第一组学生骑自行车先走，过了20分钟，第二组学生乘汽车出发，结果两组学生同学同时到达科技馆，已知第二组学生的速度是第一组学生速度的2倍，设第一组学生的速度为x千米/时，下面所列方程正确的是（ ）
A、 ﹣ = B、 =20 C、 ﹣ = D、 =208. 如图，等腰直角三角板ABC的斜边AB与量角器的直径重合，点D是量角器上60°刻度线的外端点，连接CD交AB于点E，则∠CEB的度数为（ ）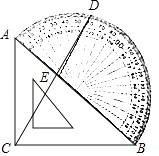
A、60° B、65° C、70° D、75°9. 如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y= 在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（ ）
A、12 B、10 C、8 D、610. 在平面直角坐标系中，若干个半径为1的单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，向右沿这条曲线做上下起伏运动（如图），点P在直线上运动的速度为每秒1个单位长度，点P在弧线上运动的速度为每秒 个单位长度，则2017秒时，点P的坐标是（ ）
A、（ ， ） B、（ ，﹣ ） C、（2017， ） D、（2017，﹣ ）二、填空题
-
11. 计算：（π﹣1）0+ = ．
12. 不等式组 的最大整数解为 ．13. 如图，在平行四边形ABCD中，连接AC，按一下步骤作图，分别以点A，点C为圆心，以大于 AC的长为半径画弧，两弧分别相交于点M、N，作直线MN交CD于点E，交AB于点F，若AB=5，BC=3，则△ADE的周长为 ．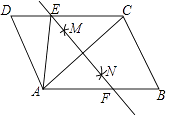
14. 如图，正方形ABCD的边长为6，分别以A、B为圆心，6为半径画 、 ，则图中阴影部分的面积为 ．
15. 如图，在直角坐标系中，点A（2，0），点B（0，1），过点A的直线l垂直于线段AB，点P是直线l上一动点，过点P作PC⊥x轴，垂足为C，把△ACP沿AP翻折180°，使点C落在点D处．若以A，D，P为顶点的三角形与△ABP相似，则所有满足此条件的点P的坐标为 ．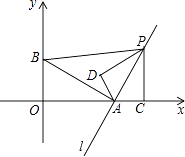
三、解答题
-
16. 先化简，再求值：
1﹣ ÷ ，其中a是方程a2﹣a﹣6=0的一个根．
17. 为了进一步贯彻落实习近平总书记关于弘扬中华优秀传统文化的指示精神，央视推出了一系列爱过益智竞赛节目，如《中国谜语大会》、《中国成语大会》、《中国汉字听写大会》、《中国诗词大会》，节目受到了广大观众的普遍欢迎，我市某校拟举行语文学科节，校语文组打算模拟其中一个节目开展一次竞赛活动，在全校范围内随机抽取了部分学生就“在这四个节目中，你最喜欢的节目是哪一个？”的问题进行了调查，要求只能从“A：《中国谜语大赛》，B：《中国成语大会》，C：《中国汉字听写大会》，D：《中国诗词大会》”中选择一个选项，他们根据调查结果，绘制成了如下两幅不完整的统计图：
请你根据图中信息，解答下列问题：
(1)、扇形统计图中，m= ， D选项所对应的圆心角度数为°；
(2)、请你补全条形统计图；
(3)、若该校共有2000名学生，请你估计其中选择D选项的学生有多少名？
(4)、若九年级一班准备从甲、乙、丙、丁四名同学中选择2名同学代表班级参加学校的比赛，请用表格或树状图分析甲和乙同学同事被选中的概率．
18. 四边形ABCD的对角线交于点E，且AE=EC，BE=ED，以AB为直径的半圆过点E，圆心为O．
(1)、利用图1，求证：四边形ABCD是菱形．
(2)、如图2，若CD的延长线与半圆相切于点F，且直径AB=8．①△ABD的面积为 ．
② 的长 ．
19. 已知关于x的方程x2﹣（2k+1）x+k2+1=0．
(1)、若方程有两个不相等的实数根，求k的取值范围；
(2)、若方程的两根恰好是一个矩形的两边长，且k=4，求该矩形的周长．
20. 如图，高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直，展开小桌板后，桌面会保持水平，其中图1、图2分别是小桌板收起时和展开时的实物，图3中的实线是小桌板展开后的示意图，其中OB表示小桌板桌面的宽度，BC表示小桌板的支架，连接OA，此时OA=75厘米，∠AOB=∠ACB=37°，且支架长BC与桌面宽OB的长度之和等于OA的长度，求点B到AC的距离．（参考数据sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
21. 近几年，全社会对空气污染问题越来越重视，空气净化器的销量也在逐年增加．某商场从厂家购进了A、B两种型号的空气净化器，两种净化器的销售相关信息见下表：A型销售数量（台）
B型销售数量（台）
总利润（元）
5
10
2000
10
5
2500
(1)、每台A型空气净化器和B型空气净化器的销售利润分别是多少？(2)、该公司计划一次购进两种型号的空气净化器共100台，其中B型空气净化器的进货量不少于A型空气净化器的2倍，为使该公司销售完这100台空气净化器后的总利润最大，请你设计相应的进货方案；(3)、已知A型空气净化器的净化能力为300m3/小时，B型空气净化器的净化能力为200m3/小时，某长方体室内活动场地的总面积为200m2 ， 室内墙高3m，该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新，若不考虑空气对流等因素，至少要购买A型空气净化器多少台？22. 问题发现：如图1，在△ABC中，∠C=90°，分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG．
(1)、△ABC与△DCF面积的关系是；（请在横线上填写“相等”或“不相等”）
(2)、拓展探究：若∠C≠90°，（1）中的结论还成立吗？若成立，请结合图2给出证明；若不成立，请说明理由；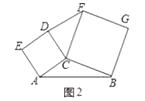
(3)、解决问题：如图3，在四边形ABCD中，AC⊥BD，且AC与BD的和为10，分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK，运用（2）的结论，图中阴影部分的面积和是否有最大值？如果有，请求出最大值，如果没有，请说明理由．
23. 如图1，抛物线y=ax2+bx+ 经过A（1，0），B（7，0）两点，交y轴于D点，以AB为边在x轴上方作等边三角形ABC．
(1)、求抛物线的解析式；
(2)、在x轴上方的抛物线上是否存在点M，是S△ABM= S△ABC？若存在，请求出点M的坐标；若不存在，请说明理由；
(3)、如图2，E是线段AC上的动点，F是线段BC上的动点，AF与BE相交于点P．①若CE=BF，试猜想AF与BE的数量关系及∠APB的度数，并说明理由；
②若AF=BE，当点E由A运动到C时，请直接写出点P经过的路径长．
