河南省安阳市2017年中考数学一模试卷
试卷更新日期：2017-11-27 类型：中考模拟
一、选择题
-
1. ﹣3的绝对值是（ ）A、﹣3 B、3 C、±3 D、﹣2. 如图，是由几个完全相同的小正方体搭建的几何体，它的左视图是（ ）
A、
B、
C、
D、
3. 下列计算正确的是（ ）A、x2•x3=x6 B、（x2）3=x5 C、x2+x3=x5 D、x6÷x3=x34. 关于x的一元二次方程ax2﹣3x+3=0有两个不等实根，则a的取值范围是（ ）
A、a＜ 且a≠0 B、a＞﹣ 且a≠0 C、a＞﹣ D、a＜5. 3月1日，河南省统计局、国家统计局河南调查总队联合公布《2016年河南省国民经济和社会发展统计公报》，《公报》显示，到2016年年末，河南省总人口为10788万人，常住人口9532万人，数据“9532万”用科学记数法可表示为（ ）A、95.32×106 B、9.532×107 C、9532×104 D、0.9532×1086. 为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则下列说法错误的是（ ）阅读量（单位：本/周）
0
1
2
3
4
人数（单位：人）
1
4
6
2
2
A、中位数是2 B、平均数是2 C、众数是2 D、极差是27. 多项式m2﹣m与多项式2m2﹣4m+2的公因式是（ ）
A、m﹣1 B、m+1 C、m2﹣1 D、（m﹣1）28. 如图所示的是A，B，C，D三点，按如下步骤作图：①先分别以A，B两点为圆心，以大于 AB的长为半径作弧，两弧相交于M、N两点，作直线MN；②再分别以B，C两点为圆心，以大于 的长为半径作弧，两弧相交于G，H两点，作直线GH，GH与MN交于点P，若∠BAC=66°，则∠BPC等于（ ）
A、100° B、120° C、132° D、140°9. 若二次函数y=﹣x2+4x+c的图象经过A（1，y1），B（﹣1，y2），C（2+ ，y3）三点，则y1、y2、y3的大小关系是（ ）
A、y1＜y2＜y3 B、y1＜y3＜y2 C、y2＜y3＜y1 D、y2＜y1＜y310. 在平面直角坐标系中，已知点A（﹣2，4），点B在直线OA上，且OA=2OB，则点B的坐标是（ ）
A、（﹣1，2） B、（1，﹣2） C、（﹣4，8） D、（﹣1，2）或（1，﹣2）二、填空题
-
11. 计算： = ．
12. 一个不透明的袋子中装有3个红球和2个白球共5个球，这些球除颜色不同外，其余均相同，从中任意摸出一个球，这个球是白球的概率为 ．
13. 如图，在菱形ABCD中，∠BAD=100°，点E为AC上一点，若∠CBE=20°，则∠AED=°．
14. 如图所示，格点△ABC绕点B逆时针旋转得到△EBD，图中每个小正方形的边长是1，则图中阴影部分的面积为 ．
15. 如图，在矩形ABCD中，AB=3，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD、AD上，则AP+PQ最小值为 ．
三、解答题
-
16. 先化简：（x﹣1﹣ ） ，然后从满足﹣2＜x≤2的整数值中选择一个你喜欢的数代入求值．17. 某中学为了搞好对“传统文化学习”的宣传活动，对本校部分学生（随机抽查）进行了一次相关知识了解程度的调查测试（成绩分为A、B、C、D、E五个组，x表示测试成绩）．通过对测试成绩的分析，得到如图所示的两幅不完整的统计图．请你根据图中提供的信息解答以下问题：
(1)、参加调查测试的学生为人；(2)、将条形统计图补充完整；(3)、本次调查测试成绩中的中位数落在组内；(4)、若测试成绩在80分以上（含80分）为优秀，该中学共有学生2600人，请你根据样本数据估计全校学生测试成绩为优秀的总人数．
18. 如图，AB为⊙O的直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，过点C作CE⊥DB交DB的延长线于点E，直线AB与CE相交于点F．
(1)、求证：CF为⊙O的切线；
(2)、填空：当∠CAB的度数为时，四边形ACFD是菱形．19. 某校兴趣小组想测量一座大楼AB的高度．如图，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1： 3 ．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， 3 ≈1.73．）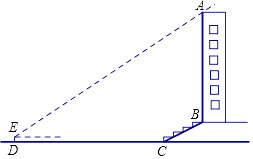
20. 如图，在平面直角坐标系中，一次函数y1=kx+b的图象分别交x轴，y轴于A、B两点，与反比例函数y2= 的图象交于C、D两点，已知点C的坐标为（﹣4，﹣1），点D的横坐标为2．
(1)、求反比例函数与一次函数的解析式；(2)、直接写出当x为何值时，y1＞y2？
(3)、点P是反比例函数在第一象限的图象上的点，且点P的横坐标大于2，过点P做x轴的垂线，垂足为点E，当△APE的面积为3时，求点P的坐标．
21. 某市决定购买A、B两种树苗对某段道路进行绿化改造，已知购买A种树苗9棵，B种树苗4棵，需要700元；购买A种树苗3棵，B种树苗5棵，则需要380元．(1)、求购买A、B两种树苗每颗各需多少元？(2)、考虑到绿化效果和资金周转，购进A种树苗不能少于60棵，且用于购买这两种树苗的资金不能超过5260元．若购进这两种树苗共100棵，则有哪几种购买方案？哪种方案最省钱？22. 已知∠ACD=90°，AC=DC，MN是过点A的直线，过点D作DB⊥MN于点B，连接CB．
(1)、问题发现如图（1），过点C作CE⊥CB，与MN交于点E，则易发现BD和EA之间的数量关系为 ， BD、AB、CB之间的数量关系为 ．
(2)、拓展探究当MN绕点A旋转到如图（2）位置时，BD、AB、CB之间满足怎样的数量关系？请写出你的猜想，并给予证明．
(3)、解决问题当MN绕点A旋转到如图（3）位置时（点C、D在直线MN两侧），若此时∠BCD=30°，BD=2时，CB= ．
23. 如图所示，抛物线y=ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
(1)、求抛物线的解析式；(2)、如图所示，直线BC下方的抛物线上有一点P，过点p作PE⊥BC于点E，作PF平行于x轴交直线BC于点F，求△PEF周长的最大值；
(3)、已知点M是抛物线的顶点，点N是y轴上一点，点Q是坐标平面内一点，若点P是抛物线上一点，且位于抛物线的对称轴右侧，是否存在以P、M、N、Q为顶点且以PM为边的正方形？若存在，直接写出点P的横坐标；若不存在，说明理由．