广东省揭阳市揭西县2017年中考数学模拟试卷
试卷更新日期：2017-11-27 类型：中考模拟
一、选择题
-
1. ﹣ 的倒数是（ ）A、﹣5 B、5 C、﹣ D、2. 如图所示，则下列选项中代表数值最小的是（ ）
A、a B、b C、﹣a D、﹣b3. 下面四个图形中，既是中心对称图形又是轴对称图形的是（ ）A、
B、
C、
D、
4. 揭西县是全国著名的侨乡，拥有海外华侨、华人及港、澳、台同胞共608000人，这一数据用科学记数法表示为（ ）A、0.608×106 B、6.08×105 C、6.08×106 D、60.8×1045. 如图所示，直线l1∥l2 ， 三角尺的一个顶点在l2上，若∠1=70°，则∠2=（ ）
A、70° B、60° C、40° D、30°6. 在中考体育测试时，有六个男生引体向上的成绩分别是：11、10、13、17、10、23，对于这组数据，下列说法不正确的是（ ）A、平均数是14 B、众数是10 C、中位数是15 D、方差是227. 已知点P（2n﹣7，4﹣2n）在第二象限，则n的取值范围是（ ）A、n＜2 B、n＞2 C、n＜ D、2＜n＜8. 如图所示，在Rt△ABC中，斜边AB=3，BC=1，点D在AB上，且 = ，则tan∠BCD的值是（ ）
A、 B、1 C、 D、9. 若二次函数y=x2﹣2x+c的图象与x轴没有交点，则c的值可能是（ ）A、﹣3 B、﹣2 C、0 D、210. 如图，点P是菱形ABCD的对角线AC上的一个动点，过点P垂直于AC的直线交菱形ABCD的边于M，N两点．设AC=2，BD=1，AP=x，△CMN的面积为y，则y关于x的函数图象大致形状是（ ）
A、
B、
C、
D、
二、填空题
-
11. 计算： ﹣6 = ．12. 分解因式：x3y﹣xy3= ．13. 分式方程 = 的解为 ．14. 如图，在直径AB=12的⊙O中，弦CD⊥AB于M，且M是半径OB的中点，则弦CD的长是（结果保留根号）．
15. 如图，在矩形ABCD中，E、F分别是AD、CD的中点，沿着BE将△ABE折叠，点A刚好落在BF上，若AB=2，则AD= ．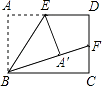
16. 如图，在正方形ABCD中，E为BC边上一点，连结AE．已知AB=8，CE=2，F是线段AE上一动点．若BF的延长线交正方形ABCD的一边于点G，且满足AE=BG，则 的值为 ．
三、解答题
-
17. 计算：（3.14﹣π）0+2cos45°﹣|1﹣ |+（ ）﹣1 ．18. 先化简，再求值： ÷（ ﹣x），其中x= ﹣2．19. 如图，已知▱ABCD．
(1)、作图，作∠A的平分线AE交CD于点E（用尺规作图法，保留作图痕迹，不要求写作法）；
(2)、在（1）的条件下，判断△AED的形状并说明理由．四、解答题（二）
-
20. 为做好“创文创卫”工作，某县城进行道路改造，由A、B两个施工队施工，已知由A施工队单独完成所有工程需要20天．若在A、B两个施工队共同施工6天后，A施工队有事撤出工程，剩下的工程由B施工队单独施工15天才完成．
(1)、求B施工队单独完成所有工程需要多少天？(2)、若施工开始后，要求B施工队施工不能超过18天，要完成该工程，A施工队至少需要施工多少天才能撤出工程？21. 如图，某校数学兴趣小组为测得大厦AB的高度，在大厦前的平地上选择一点C，测得大厦顶端A的仰角为30°，再向大厦方向前进80米，到达点D处（C，D，B三点在同一直线上），又测得大厦顶端A的仰角为45°，请你计算该大厦的高度．（精确到0.1米，参考数据： ≈1.414， ≈1.732）
22. 一个不透明的口袋中装有若干个红、黄、蓝、绿四种颜色的小球，小球除颜色外完全相同，为估计该口袋中四种颜色的小球数量，每次从口袋中随机摸出一球记下颜色并放回，重复多次试验，汇总实验结果绘制成如下不完整的条形统计图和扇形统计图．
根据以上信息解答下列问题：
(1)、求实验总次数，并补全条形统计图；(2)、扇形统计图中，摸到黄色小球次数所在扇形的圆心角度数为多少度？(3)、已知该口袋中有10个红球，请你根据实验结果估计口袋中绿球的数量．五、解答题
-
23. 如图，一次函数y=kx+b与反比例函数y= 的图象交于A（2，3），B（﹣3，n）两点．
(1)、求一次函数与反比例函数的表达式；(2)、根据所给条件，请直接写出不等式kx+b＜ 的解集；(3)、过点B作BC⊥x轴，垂足为C，求S△ABC ．24. 如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．
(1)、求证：PC是⊙O的切线；
(2)、求证：BC= AB；
(3)、点M是 的中点，CM交AB于点N，若AB=4，求MN•MC的值．
25. 在矩形ABCD中，AB=4cm，AD=6cm，延长AB到E，使BE=2AB，连接CE，动点F从A出发以2cm/s的速度沿AE方向向点E运动，动点G从E点出发，以3cm/s的速度沿E→C→D方向向点D运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止，设动点运动的时间为t秒．
(1)、当t为何值时，FC与EG互相平分；
(2)、连接FG，当t＜ 时，是否存在时间t使△EFG与△EBC相似？若存在，求出t的值；若不存在，请说明理由．
(3)、设△EFG的面积为y，求出y与t的函数关系式，求当t为何值时，y有最大值？最大值是多少？