甘肃省兰州二十八中2017年中考数学模拟试卷
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题:
-
1. 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
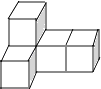 A、主视图的面积最小 B、左视图的面积最小 C、俯视图的面积最 D、三个视图的面积相等2. 一元二次方程x2+x+0.25=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定根的情况3. 抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A、y=3(x﹣1)2﹣2 B、y=3(x+1)2﹣2 C、y=3(x+1)2+2 D、y=3(x﹣1)2+24. 在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:
A、主视图的面积最小 B、左视图的面积最小 C、俯视图的面积最 D、三个视图的面积相等2. 一元二次方程x2+x+0.25=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定根的情况3. 抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A、y=3(x﹣1)2﹣2 B、y=3(x+1)2﹣2 C、y=3(x+1)2+2 D、y=3(x﹣1)2+24. 在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
A、3个 B、2个 C、1个 D、0个5. 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A,B,C和点D,E,.已知AB=1,BC=3,DE=2,则EF的长为( )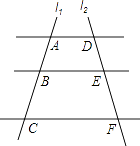 A、4 B、5 C、6 D、86. 下列语句中正确的是( )A、长度相等的两条弧是等弧 B、平分弦的直径垂直于弦 C、相等的圆心角所对的弧相等 D、经过圆心的每一条直线都是圆的对称轴7. 反比例函数y=﹣ 的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限8. 下列事件中,属于必然事件的是( )A、明天我市下雨 B、抛一枚硬币,正面朝下 C、购买一张福利彩票中奖了 D、掷一枚骰子,向上一面的数字一定大于零9. 为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )A、
A、4 B、5 C、6 D、86. 下列语句中正确的是( )A、长度相等的两条弧是等弧 B、平分弦的直径垂直于弦 C、相等的圆心角所对的弧相等 D、经过圆心的每一条直线都是圆的对称轴7. 反比例函数y=﹣ 的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限8. 下列事件中,属于必然事件的是( )A、明天我市下雨 B、抛一枚硬币,正面朝下 C、购买一张福利彩票中奖了 D、掷一枚骰子,向上一面的数字一定大于零9. 为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )A、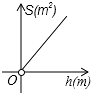 B、
B、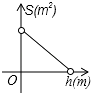 C、
C、 D、
D、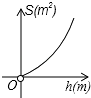 10. 某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )A、800(1+a%)2=578 B、800(1﹣a%)2=578 C、800(1﹣2a%)=578 D、800(1﹣a2%)=57811. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
10. 某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )A、800(1+a%)2=578 B、800(1﹣a%)2=578 C、800(1﹣2a%)=578 D、800(1﹣a2%)=57811. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )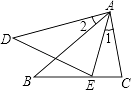 A、∠C=∠AED B、 C、∠B=∠D D、12. 正六边形的边心距为 ,则该正六边形的边长是( )A、 B、2 C、3 D、213. 图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A、∠C=∠AED B、 C、∠B=∠D D、12. 正六边形的边心距为 ,则该正六边形的边长是( )A、 B、2 C、3 D、213. 图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( ) A、y=﹣2x2 B、y=2x2 C、y=﹣ x2 D、y= x214. 两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为( )
A、y=﹣2x2 B、y=2x2 C、y=﹣ x2 D、y= x214. 两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为( )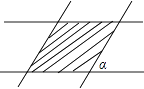 A、 B、 C、sinα D、115. 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中判断正确的有( )个.
A、 B、 C、sinα D、115. 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中判断正确的有( )个.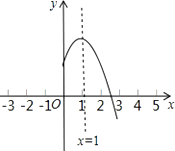 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:
-
16. 若关于x的方程(a+3)x|a|﹣1﹣3x+2=0是一元二次方程,则a的值为 .17. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为 .
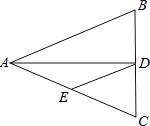 18. 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,A′相交于点D,则线段BD的长为 .
18. 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,A′相交于点D,则线段BD的长为 .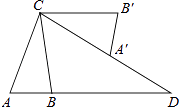 19. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
19. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .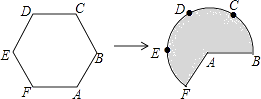 20. 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 .
20. 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 .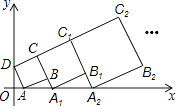
三、计算题:
-
21. 计算:3tan30°﹣2tan45°+2sin60°+4cos60°.22. 4x2﹣3=12x(用公式法解)
四、作图题:
-
23. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
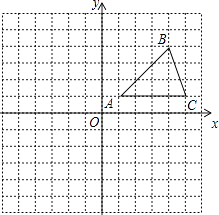
①将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2 , 并直接写出点B2、C2的坐标.五、解答题:
-
24. 将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
 (1)、这部分男生有多少人?其中成绩合格的有多少人?(2)、这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?(3)、要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.25. 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ,求旗杆AB的高度( ,结果精确到个位).
(1)、这部分男生有多少人?其中成绩合格的有多少人?(2)、这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?(3)、要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.25. 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ,求旗杆AB的高度( ,结果精确到个位). 26. 如图1,在矩形ABCD中,动点P从点A出发,沿A→D→C→B的路径运动.设点P运动的路程为x,△PAB的面积为y.图2反映的是点P在A→D→C运动过程中,y与x的函数关系.请根据图象回答以下问题:
26. 如图1,在矩形ABCD中,动点P从点A出发,沿A→D→C→B的路径运动.设点P运动的路程为x,△PAB的面积为y.图2反映的是点P在A→D→C运动过程中,y与x的函数关系.请根据图象回答以下问题: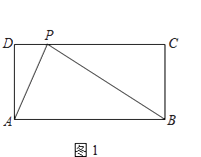 (1)、矩形ABCD的边AD= , AB=;(2)、写出点P在C→B运动过程中y与x的函数关系式,并在图2中补全函数图象.
(1)、矩形ABCD的边AD= , AB=;(2)、写出点P在C→B运动过程中y与x的函数关系式,并在图2中补全函数图象.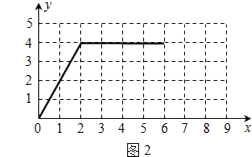 27. 如图,一次函数y1=﹣x+2的图象与反比例函数y2= 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
27. 如图,一次函数y1=﹣x+2的图象与反比例函数y2= 的图象相交于A,B两点,点B的坐标为(2m,﹣m).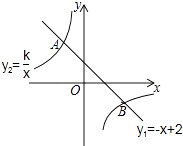 (1)、求出m值并确定反比例函数的表达式;(2)、请直接写出当x<m时,y2的取值范围.
(1)、求出m值并确定反比例函数的表达式;(2)、请直接写出当x<m时,y2的取值范围.
28. 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.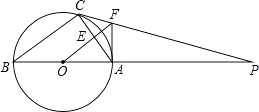 (1)、判断AF与⊙O的位置关系并说明理由;(2)、已知半径为20,AF=15,求AC的长.
(1)、判断AF与⊙O的位置关系并说明理由;(2)、已知半径为20,AF=15,求AC的长.六、综合题:
-
29. 在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
 (1)、用含x的代数式表示△MNP的面积S;(2)、当x为何值时,⊙O与直线BC相切;(3)、在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
(1)、用含x的代数式表示△MNP的面积S;(2)、当x为何值时,⊙O与直线BC相切;(3)、在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
-