安徽省宿州五中2017年中考数学一模试卷
试卷更新日期:2017-11-27 类型:中考模拟
一、选择题
-
1. 估计 的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间2. 某市举行中小学生器乐交流比赛,有45支队伍参赛,他们参赛的成绩各不相同,要取前23名获奖,某代表队已经知道了自己的成绩,他们想知道自己是否获奖,只需再知道这45支队伍成绩的( )A、中位数 B、平均数 C、最高分 D、方差3. 如图为一根圆柱形的空心钢管,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 中国高铁运营里程排世界第一,2016年,中国铁路总公司对铁路投资继续保持超8000亿元高位,8000亿用科学记数法表示为( )A、8000×108 B、8×1010 C、0.8×1011 D、8×10115. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、
4. 中国高铁运营里程排世界第一,2016年,中国铁路总公司对铁路投资继续保持超8000亿元高位,8000亿用科学记数法表示为( )A、8000×108 B、8×1010 C、0.8×1011 D、8×10115. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、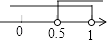 D、
D、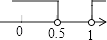 6. 下列各式中,正确的是( )A、x2•x3=x6 B、 =x C、 =x﹣1 D、x2﹣x+1=(x﹣ )2+7. 将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( )
6. 下列各式中,正确的是( )A、x2•x3=x6 B、 =x C、 =x﹣1 D、x2﹣x+1=(x﹣ )2+7. 将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( ) A、50° B、110° C、130° D、150°8. 如图,用相同的小正方形按照某种规律进行摆放,则第8个图形中小正方形的个数是( )
A、50° B、110° C、130° D、150°8. 如图,用相同的小正方形按照某种规律进行摆放,则第8个图形中小正方形的个数是( ) A、71 B、78 C、85 D、899. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥1时,y随x的增大而减小 D、若a<0,则当x≤1时,y随x的增大而增大10. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1 , 且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )
A、71 B、78 C、85 D、899. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥1时,y随x的增大而减小 D、若a<0,则当x≤1时,y随x的增大而增大10. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1 , 且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( ) A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
11. 分解因式:a2b+2ab2+b3= .12. 某快递公司的分拣工小王和小李,在分拣同一类物件时,小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同.已知小王每小时比小李多分拣8个物件,设小李每小时分拣x个物件,根据题意列出的方程是 .13. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 上的一点,BD交AC于点E,若BC=4,AD= ,则AE的长是 .
 14. 反比例函数y1= (a>0,a为常数)和y2= 在第一象限内的图象如图所示,点M在y2= 的图象上,MC⊥x轴于点C,交y1= 的图象于点A;MD⊥y轴于点D,交y1= 的图象于点B,当点M在y2= 的图象上运动时,以下结论:
14. 反比例函数y1= (a>0,a为常数)和y2= 在第一象限内的图象如图所示,点M在y2= 的图象上,MC⊥x轴于点C,交y1= 的图象于点A;MD⊥y轴于点D,交y1= 的图象于点B,当点M在y2= 的图象上运动时,以下结论:①S△ODB=S△OCA;
②四边形OAMB的面积为2﹣a;
③当a=1时,点A是MC的中点;
④若S四边形OAMB=S△ODB+S△OCA , 则四边形OCMD为正方形.
其中正确的是 . (把所有正确结论的序号都填在横线上)

三、解答题
-
15. 计算:(π﹣4)0+|3﹣tan60°|﹣( )﹣2+ .
16. 解方程组: .四、解答题
-
17. 小丹、小林是某中学八年级的同班同学,在升入九年级时,学校打算重新组班,他们将被随机编入A,B,C三个班.(1)、请你用画树状图法或列表法,列出所有可能的结果;(2)、求两人再次成为同班同学的概率.18. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
 (1)、画出△ABC绕点O顺时针旋转90°后的△A1B1C1;(2)、求△OAA1的面积.
(1)、画出△ABC绕点O顺时针旋转90°后的△A1B1C1;(2)、求△OAA1的面积.五、解答题
-
19. 某地2014年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2016年在2014年的基础上增加投入资金1600万元.(1)、从2014年到2016年,该地投入异地安置资金的年平均增长率为多少?(2)、在2016年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
20. 图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响),由光源O射出的光线沿灯罩形成光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°, (1)、求该台灯照亮桌面的宽度BC(不考虑其他因素,结果精确到1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ≈1.73)
(1)、求该台灯照亮桌面的宽度BC(不考虑其他因素,结果精确到1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ≈1.73)
(2)、若灯臂最长可伸长至60cm,不调整灯罩的角度,能否让台灯照亮桌面85cm的宽度?
六、解答题
-
21. 已知反比例函数y= 的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F
 (1)、当 = 且△OFE的面积等于 时,求这个一次函数的解析式;
(1)、当 = 且△OFE的面积等于 时,求这个一次函数的解析式;
(2)、在(1)的条件下,根据函数图象,试求不等式 >kx+b的解集.
七、解答题
-
22. 如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
 (1)、点P的坐标为;
(1)、点P的坐标为;
(2)、求抛物线L的解析式;
(3)、求△OAE与△OCE面积之和的最大值.
八、解答题
-
23. 【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.(1)、某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: = ;
 (2)、【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 = ,则 的值为;
(2)、【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 = ,则 的值为; (3)、【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
(3)、【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
-
-