2016年浙江省义乌市中考数学试卷

试卷更新日期：2016-09-12 类型：中考真卷

进入出卷网下载

一、单选题

1. ﹣8的绝对值等于（）

A、8 B、﹣8 C、- $\frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为（）

A、3.386×10⁸ B、0.3386×10⁹ C、33.86×10⁷ D、3.386×10⁹

查看试题解析
3. 我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化，窗框一部分如图2，它是一个轴对称图形，其对称轴有（）

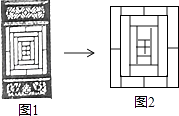A、1条 B、2条 C、3条 D、4条

查看试题解析
4. 如图是一个正方体，则它的表面展开图可以是（）

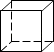A、 B、 C、 D、

查看试题解析
5. 一枚质地均匀的骰子，其六个面上分别标有数字1，2，3，4，5，6，投掷一次，朝上一面的数字是偶数的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，BD是⊙O的直径，点A、C在⊙O上， = ，∠AOB=60°，则∠BDC的度数是（）

A、60° B、45° C、35° D、30°

查看试题解析
7. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
8.
如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（）

A、 $\frac{\sqrt{3}}{12}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
9. 抛物线y=x²+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，则c的值不可能是（）

A、4 B、6 C、8 D、10

查看试题解析
10.
我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（）

A、84 B、336 C、510 D、1326

查看试题解析

二、填空题（本大题有6小题，每小题5分，共30分）

11. 分解因式：a³﹣9a= ．

查看试题解析
12. 不等式 $\frac{3 x + 13}{4}$ ＞ $\frac{x}{3}$ +2的解是．

查看试题解析
13. 如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为 cm．

查看试题解析
14. 书店举行购书优惠活动：
①一次性购书不超过100元，不享受打折优惠；
②一次性购书超过100元但不超过200元一律打九折；
③一次性购书超过200元一律打七折．
小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是元．

查看试题解析
15.
如图，已知直线l：y=﹣x，双曲线y= $\frac{1}{x}$ ，在l上取一点A（a，﹣a）（a＞0），过A作x轴的垂线交双曲线于点B，过B作y轴的垂线交l于点C，过C作x轴的垂线交双曲线于点D，过D作y轴的垂线交l于点E，此时E与A重合，并得到一个正方形ABCD，若原点O在正方形ABCD的对角线上且分这条对角线为1：2的两条线段，则a的值为．

查看试题解析
16. 如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为．

查看试题解析

三、解答题

17. 计算与解方程．

(1)、计算： $\frac{5}{\sqrt{5}}$ ﹣（2﹣ $\sqrt{5}$ ）⁰+（ $\frac{1}{2}$ ）^﹣² ．

(2)、解分式方程： $\frac{x}{x - 1}$ + $\frac{2}{1 - x}$ =4．

查看试题解析
18. 为了解七年级学生上学期参加社会实践活动的情况，随机抽查A市七年级部分学生参加社会实践活动天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．
A市七年级部分学生参加社会实践活动天数的频数分布表
天数
频数
频率
3
20
0.10
4
30
0.15
5
60
0.30
6
a
0.25
7
40
0.20
A市七年级部分学生参加社会实践活动天数的条形统计图
根据以上信息，解答下列问题；

(1)、求出频数分布表中a的值，并补全条形统计图．

(2)、A市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．

查看试题解析
19. 根据卫生防疫部门要求，游泳池必须定期换水，清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q（m²）和开始排水后的时间t（h）之间的函数图象如图所示，根据图象解答下列问题：

(1)、暂停排水需要多少时间？排水孔排水速度是多少？

(2)、当2≤t≤3.5时，求Q关于t的函数表达式．

查看试题解析
20. 如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60m到达C点，测得点B在点C的北偏东60°方向，如图2．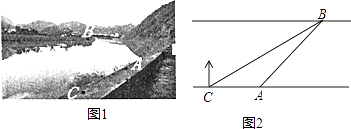

(1)、求∠CBA的度数．

(2)、求出这段河的宽（结果精确到1m，备用数据 $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）．

查看试题解析
21.
课本中有一个例题：
有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？
这个例题的答案是：当窗户半圆的半径约为0.35m时，透光面积最大值约为1.05m² ．
我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m，利用图3，解答下列问题：

(1)、若AB为1m，求此时窗户的透光面积？

(2)、与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．

查看试题解析
22. 如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．

(1)、若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．

(2)、若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．

查看试题解析
23.
对于坐标平面内的点，现将该点向右平移1个单位，再向上平移2的单位，这种点的运动称为点A的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5），已知点A的坐标为（1，0）．

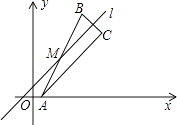(1)、分别写出点A经1次，2次斜平移后得到的点的坐标．

(2)、如图，点M是直线l上的一点，点A关于点M的对称点的点B，点B关于直线l的对称轴为点C．
①若A、B、C三点不在同一条直线上，判断△ABC是否是直角三角形？请说明理由．
②若点B由点A经n次斜平移后得到，且点C的坐标为（7，6），求出点B的坐标及n的值．

查看试题解析
24.
如图，在矩形ABCD中，点O为坐标原点，点B的坐标为（4，3），点A、C在坐标轴上，点P在BC边上，直线l₁：y=2x+3，直线l₂：y=2x﹣3．

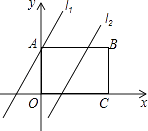(1)、分别求直线l₁与x轴，直线l₂与AB的交点坐标；

(2)、已知点M在第一象限，且是直线l₂上的点，若△APM是等腰直角三角形，求点M的坐标；

(3)、我们把直线l₁和直线l₂上的点所组成的图形为图形F．已知矩形ANPQ的顶点N在图形F上，Q是坐标平面内的点，且N点的横坐标为x，请直接写出x的取值范围（不用说明理由）．

查看试题解析

天数	频数	频率
3	20	0.10
4	30	0.15
5	60	0.30
6	a	0.25
7	40	0.20