2016年天津市中考数学试卷

试卷更新日期：2016-09-12 类型：中考真卷

进入出卷网下载

一、选择题：

1. 计算（﹣2）﹣5的结果等于（）

A、﹣7 B、﹣3 C、3 D、7

查看试题解析
2. sin60°的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
3. 下列图形中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 2016年5月24日《天津日报》报道，2015年天津外环线内新栽植树木6120000株，将6120000用科学记数法表示应为（）

A、0.612×10⁷ B、6.12×10⁶ C、61.2×10⁵ D、612×10⁴

查看试题解析
5.
如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）

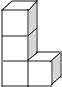A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{19}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 计算 $\frac{x + 1}{x}$ ﹣ $\frac{1}{x}$ 的结果为（）

A、1 B、x C、 $\frac{1}{x}$ D、 $\frac{x + 2}{x}$

查看试题解析
8. 方程x²+x﹣12=0的两个根为（）

A、x₁=﹣2，x₂=6 B、x₁=﹣6，x₂=2 C、x₁=﹣3，x₂=4 D、x₁=﹣4，x₂=3

查看试题解析
9. 实数a，b在数轴上的对应点的位置如图所示，把﹣a，﹣b，0按照从小到大的顺序排列，正确的是（）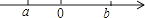

A、﹣a＜0＜﹣b B、0＜﹣a＜﹣b C、﹣b＜0＜﹣a D、0＜﹣b＜﹣a

查看试题解析
10. 如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）

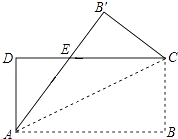A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE

查看试题解析
11. 若点A（﹣5，y₁），B（﹣3，y₂），C（2，y₃）在反比例函数y= $\frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₃＜y₂ B、y₁＜y₂＜y₃ C、y₃＜y₂＜y₁ D、y₂＜y₁＜y₃

查看试题解析
12. 已知二次函数y=（x﹣h）²+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）

A、1或﹣5 B、﹣1或5 C、1或﹣3 D、1或3

查看试题解析

二、填空题：

13. 计算（2a）³的结果等于．

查看试题解析
14. 计算（ $\sqrt{5}$ + $\sqrt{3}$ ）（ $\sqrt{5}$ ﹣ $\sqrt{3}$ ）的结果等于．

查看试题解析
15. 不透明袋子中装有6个球，其中有1个红球、2个绿球和3个黑球，这些球除颜色外无其他差别，从袋子中随机取出1个球，则它是绿球的概率是．

查看试题解析
16. 若一次函数y=﹣2x+b（b为常数）的图象经过第二、三、四象限，则b的值可以是（写出一个即可）．

查看试题解析
17. 如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则 $\frac{S_{正方形 M N P Q}}{S_{正方形 A E F G}}$ 的值等于．

查看试题解析
18.
如图，在每个小正方形的边长为1的网格中，A，E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点．

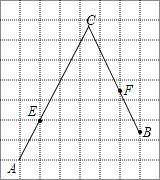(1)、AE的长等于；

(2)、若点P在线段AC上，点Q在线段BC上，且满足AP=PQ=QB，请在如图所示的网格中，用无刻度的直尺，画出线段PQ，并简要说明点P，Q的位置是如何找到的（不要求证明）．

查看试题解析

三、综合题：

19. 解不等式组 ${\begin{matrix} x + 2 \leq 6 ① \\ 3 x - 2 \geq 2 x ② \end{matrix}$ ，请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、
把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
20. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：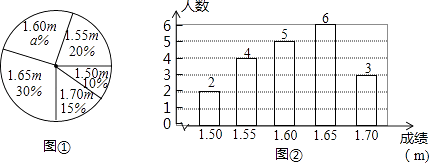

(1)、图1中a的值为；

(2)、求统计的这组初赛成绩数据的平均数、众数和中位数；

(3)、根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

查看试题解析
21. 在⊙O中，AB为直径，C为⊙O上一点．

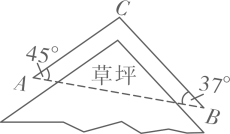
(1)、如图1．过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=27°，求∠P的大小；

(2)、如图2，D为上一点，且OD经过AC的中点E，连接DC并延长，与AB的延长线相交于点P，若∠CAB=10°，求∠P的大小．

查看试题解析
22. 小明上学途中要经过A，B两地，由于A，B两地之间有一片草坪，所以需要走路线AC，CB，如图，在△ABC中，AB=63m，∠A=45°，∠B=37°，求AC，CB的长．（结果保留小数点后一位）
参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{2}$ 取1.414．

查看试题解析
23. 公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元

(1)、设租用甲种货车x辆（x为非负整数），试填写表格．
表一：
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二：
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2800
租用乙种货车的费用/元
280

(2)、给出能完成此项运送任务的最节省费用的租车方案，并说明理由．

查看试题解析
24.
在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．

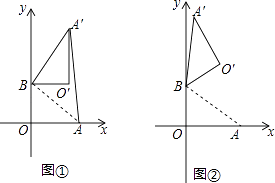(1)、如图①，若α=90°，求AA′的长；

(2)、如图②，若α=120°，求点O′的坐标；

(3)、在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，求点P′的坐标（直接写出结果即可）

查看试题解析
25. 已知抛物线C：y=x²﹣2x+1的顶点为P，与y轴的交点为Q，点F（1， $\frac{1}{2}$ ）．

(1)、求点P，Q的坐标；

(2)、将抛物线C向上平移得到抛物线C′，点Q平移后的对应点为Q′，且FQ′=OQ′．
①求抛物线C′的解析式；
②若点P关于直线Q′F的对称点为K，射线FK与抛物线C′相交于点A，求点A的坐标．

查看试题解析

租用甲种货车的数量/辆	3	7	x
租用的甲种货车最多运送机器的数量/台	135
租用的乙种货车最多运送机器的数量/台	150

租用甲种货车的数量/辆	3	7	x
租用甲种货车的费用/元		2800
租用乙种货车的费用/元		280