2016年四川省雅安市中考数学试卷

试卷更新日期：2016-09-12 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2016的相反数是（）

A、﹣2016 B、2016 C、﹣ $\frac{1}{2016}$ D、 $\frac{1}{2016}$

查看试题解析
2. 下列各式计算正确的是（）

A、（a+b）²=a²+b² B、x²•x³=x⁶ C、x²+x³=x⁵ D、（a³）³=a⁹

查看试题解析
3. 已知a²+3a=1，则代数式2a²+6a﹣1的值为（）

A、0 B、1 C、2 D、3

查看试题解析
4. 已知△ABC顶点坐标分别是A（0，6），B（﹣3，﹣3），C（1，0），将△ABC平移后顶点A的对应点A₁的坐标是（4，10），则点B的对应点B₁的坐标为（）

A、（7，1） B、B（1，7） C、（1，1） D、（2，1）

查看试题解析
5.
将如图绕AB边旋转一周，所得几何体的俯视图为（）

A、 B、 C、 D、

查看试题解析
6. 某校为开展第二课堂，组织调查了本校150名学生各自最喜爱的一项体育活动，制成了如下扇形统计图，则在该被调查的学生中，跑步和打羽毛球的学生人数分别是（）

A、30，40 B、45，60 C、30，60 D、45，40

查看试题解析
7. 已知关于x的一元二次方程x²+mx﹣8=0的一个实数根为2，则另一实数根及m的值分别为（）

A、4，﹣2 B、﹣4，﹣2 C、4，2 D、﹣4，2

查看试题解析
8. 如图所示，底边BC为2 $\sqrt{3}$ ，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）

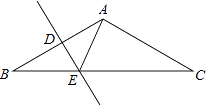A、2+2 $\sqrt{3}$ B、2+ $\sqrt{3}$ C、4 D、3 $\sqrt{3}$

查看试题解析
9. 如图，四边形ABCD的四边相等，且面积为120cm² ，对角线AC=24cm，则四边形ABCD的周长为（）

A、52cm B、40cm C、39cm D、26cm

查看试题解析
10. “一方有难，八方支援”，雅安芦山4•20地震后，某单位为一中学捐赠了一批新桌椅，学校组织初一年级200名学生搬桌椅．规定一人一次搬两把椅子，两人一次搬一张桌子，每人限搬一次，最多可搬桌椅（一桌一椅为一套）的套数为（）

A、60 B、70 C、80 D、90

查看试题解析
11. 若式子 $\sqrt{k- 1}$ +（k﹣1）⁰有意义，则一次函数y=（1﹣k）x+k﹣1的图象可能是（）

A、 B、 C、 D、

查看试题解析
12. 如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、2 $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析

二、填空题

13. 1.45°= ．

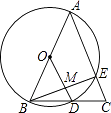
查看试题解析
14. P为正整数，现规定P!=P（P﹣1）（P﹣2）…×2×1．若m!=24，则正整数m= ．

查看试题解析
15. 一书架有上下两层，其中上层有2本语文1本数学，下层有2本语文2本数学，现从上下层随机各取1本，则抽到的2本都是数学书的概率为．

查看试题解析
16. 如图，在△ABC中，AB=AC=10，以AB为直径的⊙O与BC交于点D，与AC交于点E，连OD交BE于点M，且MD=2，则BE长为．

查看试题解析
17. 已知a+b=8，a²b²=4，则 $\frac{a^{2} + b^{2}}{2}$ ﹣ab= ．

查看试题解析

三、解答题

18. 计算

(1)、计算：﹣2²+（﹣ $\frac{1}{3}$ ）^﹣¹+2sin60°﹣|1﹣ $\sqrt{3}$ |

(2)、先化简，再求值：（ $\frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ﹣x﹣1）÷ $\frac{x + 1}{x - 1}$ ，其中x=﹣2．

查看试题解析
19. 解下列不等式组，并将它的解集在数轴上表示出来．
${\begin{matrix} x - 1 > 2 x \\ \frac{x - 1}{3} \leq \frac{x + 1}{9} \end{matrix}$ ．

查看试题解析
20. 甲乙两人进行射击训练，两人分别射击12次，如图分别统计了两人的射击成绩，已知甲射击成绩的方差S_甲²= $\frac{7}{12}$ ，平均成绩 $\bar{x 甲}$ =8.5．

(1)、根据图上信息，估计乙射击成绩不少于9环的概率是多少？

(2)、求乙射击的平均成绩的方差，并据此比较甲乙的射击“水平”．
S²= $\frac{1}{n}$ [（x₁﹣ $\vec{x}$ ）²+（x₂﹣ $\vec{x}$ ）²…（x_n﹣ $\vec{x}$ ）²]．

查看试题解析
21. 我们规定：若 $\vec{m}$ =（a，b）， $\vec{n}$ =（c，d），则 $\vec{m} \cdot \vec{n}$ =ac+bd．如 $\vec{m}$ =（1，2）， $\vec{n}$ =（3，5），则 $\vec{m} \cdot \vec{n}$ =1×3+2×5=13．

(1)、已知 $\vec{m}$ =（2，4）， $\vec{n}$ =（2，﹣3），求 $\vec{m} \cdot \vec{n}$ ；

(2)、已知 $\vec{m}$ =（x﹣a，1）， $\vec{n}$ =（x﹣a，x+1），求y= $\vec{m} \cdot \vec{n}$ ，问y= $\vec{m} \cdot \vec{n}$ 的函数图象与一次函数y=x﹣1的图象是否相交，请说明理由．

查看试题解析
22. 已知Rt△ABC中，∠B=90°，AC=20，AB=10，P是边AC上一点（不包括端点A、C），过点P作PE⊥BC于点E，过点E作EF∥AC，交AB于点F．设PC=x，
PE=y．

(1)、求y与x的函数关系式；

(2)、是否存在点P使△PEF是Rt△？若存在，求此时的x的值；若不存在，请说明理由．

查看试题解析
23.
已知直线l₁：y=x+3与x轴交于点A，与y轴交于点B，且与双曲线y= $\frac{k}{x}$ 交于点C（1，a）．

(1)、试确定双曲线的函数表达式；

(2)、将l₁沿y轴翻折后，得到l₂ ，画出l₂的图象，并求出l₂的函数表达式；

(3)、在（2）的条件下，点P是线段AC上点（不包括端点），过点P作x轴的平行线，分别交l₂于点M，交双曲线于点N，求S_△_AMN的取值范围．

查看试题解析
24. 如图1，AB是⊙O的直径，E是AB延长线上一点，EC切⊙O于点C，OP⊥AO交AC于点P，交EC的延长线于点D．

(1)、求证：△PCD是等腰三角形；

(2)、CG⊥AB于H点，交⊙O于G点，过B点作BF∥EC，交⊙O于点F，交CG于Q点，连接AF，如图2，若sinE= $\frac{3}{5}$ ，CQ=5，求AF的值．

查看试题解析