2016年广西贵港市中考数学试卷
试卷更新日期:2016-09-12 类型:中考真卷
一、每小题都给出标号为(A)、(B)、(C)、(D)的四个选项,其中只有一个是正确的.请考生用2B铅笔在答题卡上将选定的答案标号涂黑.
-
1. ﹣2的绝对值是( )A、2 B、﹣2 C、0 D、12. 下列运算正确的是( )A、3a+2b=5ab B、3a•2b=6ab C、(a3)2=a5 D、(ab2)3=ab63. 用科学记数法表示的数是1.69×105 , 则原来的数是( )A、169 B、1690 C、16900 D、1690004. 在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )A、35° B、40° C、45° D、50°5. 式子 在实数范围内有意义,则x的取值范围是( )A、x<1 B、x≤1 C、x>1 D、x≥16. 在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )A、(﹣1,1) B、(﹣1,﹣2) C、(﹣1,2) D、(1,2)7. 从﹣ ,0, ,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是( )A、 B、 C、 D、8. 下列命题中错误的是( )A、两组对角分别相等的四边形是平行四边形 B、矩形的对角线相等 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形9. 若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 + 的值是( )A、3 B、﹣3 C、5 D、﹣510.
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2 ,则这个圆锥底面圆的半径是( )
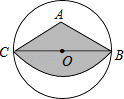 A、 B、 C、 D、11. 如图,抛物线y=﹣ x2+ x+ 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
A、 B、 C、 D、11. 如图,抛物线y=﹣ x2+ x+ 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )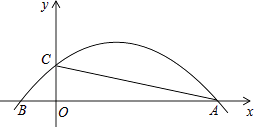 A、(4,3) B、(5, ) C、(4, ) D、(5,3)12. 如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
A、(4,3) B、(5, ) C、(4, ) D、(5,3)12. 如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6;④S△OCF=2S△OEF
成立的个数有( )
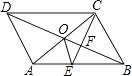 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 8的立方根是 .14. 分解因式:a2b﹣b= .15. 如图,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2的度数是 .
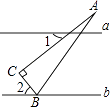 16. 如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .
16. 如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .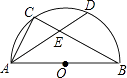 17. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).
17. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).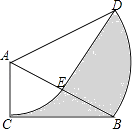 18. 已知a1= ,a2= ,a3= ,…,an+1= (n为正整数,且t≠0,1),则a2016=(用含有t的代数式表示).
18. 已知a1= ,a2= ,a3= ,…,an+1= (n为正整数,且t≠0,1),则a2016=(用含有t的代数式表示).三、解答题
-
19. 计算与解方程.(1)、计算:( )﹣1﹣ ﹣(π﹣2016)0+9tan30°;(2)、解分式方程: +1= .20. 如图,在▱ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
 (1)、用无刻度的直尺画出△ABC的高CH(保留画图痕迹);(2)、求△ACE的面积.21. 如图,已知一次函数y= x+b的图象与反比例函数y= (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)、用无刻度的直尺画出△ABC的高CH(保留画图痕迹);(2)、求△ACE的面积.21. 如图,已知一次函数y= x+b的图象与反比例函数y= (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上. (1)、当△ABC的周长最小时,求点C的坐标;(2)、当 x+b< 时,请直接写出x的取值范围.22. 在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)、当△ABC的周长最小时,求点C的坐标;(2)、当 x+b< 时,请直接写出x的取值范围.22. 在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题: (1)、本次接受问卷调查的学生总人数是;(2)、扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为;(3)、若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.23. 为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.(1)、求2014至2016年该市投入科研经费的年平均增长率;(2)、根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.24. 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)、本次接受问卷调查的学生总人数是;(2)、扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为;(3)、若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.23. 为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.(1)、求2014至2016年该市投入科研经费的年平均增长率;(2)、根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.24. 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.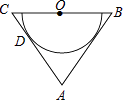 (1)、求证:AB是半圆O所在圆的切线;(2)、若cos∠ABC= ,AB=12,求半圆O所在圆的半径.25.
(1)、求证:AB是半圆O所在圆的切线;(2)、若cos∠ABC= ,AB=12,求半圆O所在圆的半径.25.如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
 (1)、求该抛物线的解析式;(2)、若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.26.
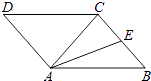
(1)、求该抛物线的解析式;(2)、若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.26.如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
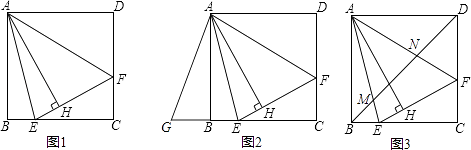 (1)、如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)、如图2,将△ADF绕点A顺时针旋转90°得到△ABG.①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)、如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.