相似常考题型
试卷更新日期:2017-11-24 类型:复习试卷
一、单选题
-
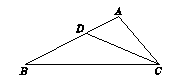
1. 如图,△ABC中,AD是中线,BC=10,∠B=∠DAC,则线段AC的长为( )
 A、4 B、5 C、5 D、52. 如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( )
A、4 B、5 C、5 D、52. 如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( )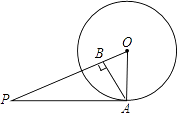 A、16cm B、48cm C、6 cm D、4 cm3. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )
A、16cm B、48cm C、6 cm D、4 cm3. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )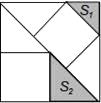 A、1: B、1:2 C、2:3 D、4:94.
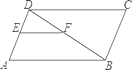
A、1: B、1:2 C、2:3 D、4:94.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=6,则CD的长为( )
 A、14 B、17 C、8 D、125. 将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A、14 B、17 C、8 D、125. 将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )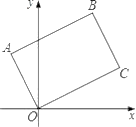 A、(4,2) B、(2,4) C、( ,3) D、(3, )6. 如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A、(4,2) B、(2,4) C、( ,3) D、(3, )6. 如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A、1:25 B、1:5 C、1:2.5 D、1:7. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )来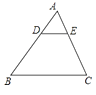 A、
A、 B、
B、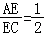 C、
C、 D、
D、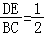 8. 如图,点D在 的边AC上,要判断 与 相似,添加一个条件,不正确的是( )
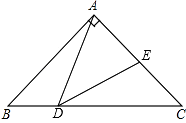
8. 如图,点D在 的边AC上,要判断 与 相似,添加一个条件,不正确的是( ) A、 B、 C、 D、9. 如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A、 B、 C、 D、9. 如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )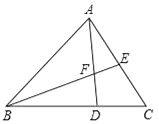 A、△BDF∽△BEC B、△BFA∽△BEC C、△BAC∽△BDA D、△BDF∽△BAE10. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A、△BDF∽△BEC B、△BFA∽△BEC C、△BAC∽△BDA D、△BDF∽△BAE10. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )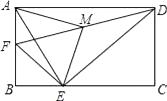 A、5 B、 C、 D、
A、5 B、 C、 D、二、填空题
-
11. 如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC= .
 12. 若 = = =3(b+d+f≠0),则 = .13. 已知: ,则 = .14. 已知a、b、d、c是成比例线段,a=4cm,b=6cm,d=9cm,则c= .15. 若线段x是9和16的比例中项,则线段x的值为 .16. 在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
12. 若 = = =3(b+d+f≠0),则 = .13. 已知: ,则 = .14. 已知a、b、d、c是成比例线段,a=4cm,b=6cm,d=9cm,则c= .15. 若线段x是9和16的比例中项,则线段x的值为 .16. 在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)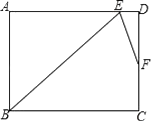 17. 如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是 .
17. 如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是 . 18. 在△ABC和△A1B1C1中,若 ,且∠B=∠B1=56°,则 =。19. 若 ,则 的值为 .20. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .
18. 在△ABC和△A1B1C1中,若 ,且∠B=∠B1=56°,则 =。19. 若 ,则 的值为 .20. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .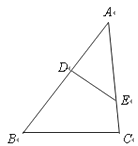
三、解答题
-
21. 如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BD•CE,求证:△ABD∽△ECA.
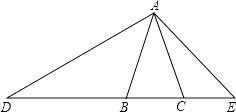 22. 已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?
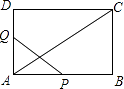
22. 已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?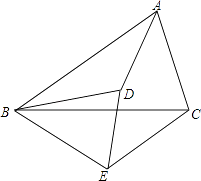 23. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.
23. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.