2016年浙江省湖州市中考数学试卷
试卷更新日期:2016-09-09 类型:中考真卷
一、选择题
-
1. 计算(﹣20)+16的结果是( )A、﹣4 B、4 C、﹣2016 D、20162. 为了迎接杭州G20峰会,某校开展了设计“YJG20”图标的活动,下列图形中及时轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 由六个相同的立方体搭成的几何体如图所示,则它的主视图是( )
3. 由六个相同的立方体搭成的几何体如图所示,则它的主视图是( )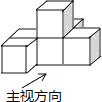 A、
A、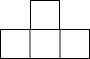 B、
B、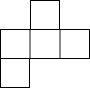 C、
C、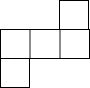 D、
D、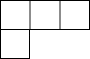 4. 受“乡村旅游第一市”的品牌效应和2015年国际乡村旅游大会的宣传效应的影响,2016年湖州市在春节黄金周期间共接待游客约2800000人次,同比增长约56%,将2800000用科学记数法表示应是( )A、28×105 B、2.8×106 C、2.8×105 D、0.28×1055. 数据1,2,3,4,4,5的众数是( )A、5 B、3 C、3.5 D、46. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
4. 受“乡村旅游第一市”的品牌效应和2015年国际乡村旅游大会的宣传效应的影响,2016年湖州市在春节黄金周期间共接待游客约2800000人次,同比增长约56%,将2800000用科学记数法表示应是( )A、28×105 B、2.8×106 C、2.8×105 D、0.28×1055. 数据1,2,3,4,4,5的众数是( )A、5 B、3 C、3.5 D、46. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( ) A、8 B、6 C、4 D、27. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣4|,则其结果恰为2的概率是( )A、 B、 C、 D、8. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A、8 B、6 C、4 D、27. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣4|,则其结果恰为2的概率是( )A、 B、 C、 D、8. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )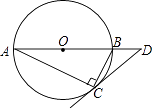 A、25° B、40° C、50° D、65°9. 定义:若点P(a,b)在函数y= 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= 的一个“派生函数”.例如:点(2, )在函数y= 的图象上,则函数y=2x2+ x称为函数y= 的一个“派生函数”.现给出以下两个命题:(1)存在函数y= 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= 的所有“派生函数”,的图象都进过同一点.
A、25° B、40° C、50° D、65°9. 定义:若点P(a,b)在函数y= 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= 的一个“派生函数”.例如:点(2, )在函数y= 的图象上,则函数y=2x2+ x称为函数y= 的一个“派生函数”.现给出以下两个命题:(1)存在函数y= 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= 的所有“派生函数”,的图象都进过同一点.下列判断正确的是( )
A、命题(1)与命题(2)都是真命题 B、命题(1)与命题(2)都是假命题 C、命题(1)是假命题,命题(2)是真命题 D、命题(1)是真命题,命题(2)是假命题10. 如图1,在等腰三角形ABC中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( )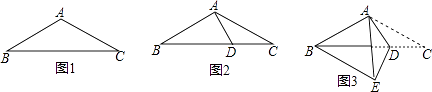 A、4 B、 C、3 D、2
A、4 B、 C、3 D、2二、填空题
-
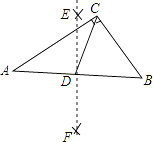
11. 数5的相反数是 .12. 方程 =1的根是x= .13. 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 .
 14. 如图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是度.
14. 如图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是度.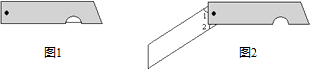 15. 已知四个有理数a,b,x,y同时满足以下关系式:b>a,x+y=a+b,y﹣x<a﹣b.请将这四个有理数按从小到大的顺序用“<”连接起来是 .16. 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)、k的值是;(2)、如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y= 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是 .
15. 已知四个有理数a,b,x,y同时满足以下关系式:b>a,x+y=a+b,y﹣x<a﹣b.请将这四个有理数按从小到大的顺序用“<”连接起来是 .16. 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)、k的值是;(2)、如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y= 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是 .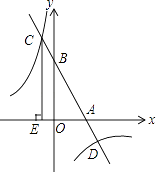
三、解答题
-
17. 计算:tan45°﹣sin30°+(2﹣ )0 .18. 当a=3,b=﹣1时,求下列代数式的值.(1)、(a+b)(a﹣b);(2)、a2+2ab+b2 .19. 湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘.(1)、求鱼塘的长y(米)关于宽x(米)的函数表达式;(2)、由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米,鱼塘的长为多少米?20. 如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
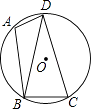 (1)、求证:BD=CD;(2)、若圆O的半径为3,求
(1)、求证:BD=CD;(2)、若圆O的半径为3,求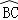 的长. 21. 中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
的长. 21. 中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:抽取的200名学生海选成绩分组表
组别
海选成绩x
A组
50≤x<60
B组
60≤x<70
C组
70≤x<80
D组
80≤x<90
E组
90≤x<100
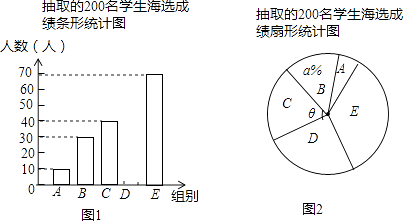
请根据所给信息,解答下列问题:
(1)、请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(2)、在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;(3)、规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?22. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;(2)、若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?23. 如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.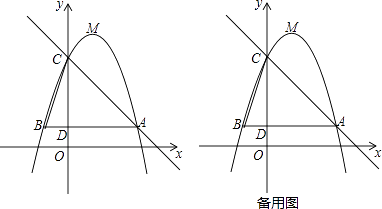 (1)、求该二次函数的解析式及点M的坐标;(2)、若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)、点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).24. 数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)、求该二次函数的解析式及点M的坐标;(2)、若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)、点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).24. 数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).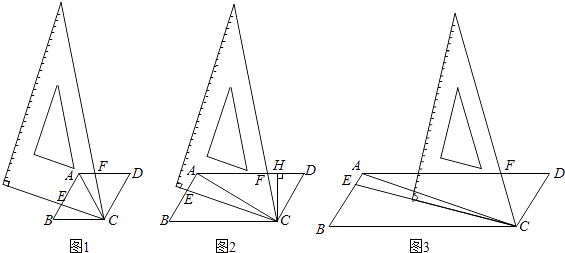 (1)、初步尝试
(1)、初步尝试如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)、类比发现如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)、深入探究如图3,若AD=3AB,探究得: 的值为常数t,则t= .