2016年云南省昆明市中考数学试卷

试卷更新日期：2016-09-09 类型：中考真卷

进入出卷网下载

一、填空题：

1. ﹣4的相反数为．

查看试题解析
2. 昆明市2016年参加初中学业水平考试的人数约有67300人，将数据67300用科学记数法表示为．

查看试题解析
3. 计算： $\frac{2 x}{x^{2} - y^{2}}$ ﹣ $\frac{2 y}{x^{2} - y^{2}}$ = ．

查看试题解析
4.
如图，AB∥CE，BF交CE于点D，DE=DF，∠F=20°，则∠B的度数为．

查看试题解析
5.
如图，E，F，G，H分别是矩形ABCD各边的中点，AB=6，BC=8，则四边形EFGH的面积是．

查看试题解析
6.
如图，反比例函数y= $\frac{k}{x}$ （k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为．

查看试题解析

二、选择题

7.
下面所给几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
8. 某学习小组9名学生参加“数学竞赛”，他们的得分情况如表：
人数（人）
1
3
4
1
分数（分）
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是（）

A、90，90 B、90，85 C、90，87 D、85，85

查看试题解析
9. 一元二次方程x²﹣4x+4=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
10. 不等式组 ${\begin{matrix} x - 3 < 1 \\ 3 x + 2 \leq 4 x \end{matrix}$ 的解集为（）

A、x≤2 B、x＜4 C、2≤x＜4 D、x≥2

查看试题解析
11. 下列运算正确的是（）

A、（a﹣3）²=a²﹣9 B、a²•a⁴=a⁸ C、 $\sqrt{9}$ =±3 D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
12.
如图，AB为⊙O的直径，AB=6，AB⊥弦CD，垂足为G，EF切⊙O于点B，∠A=30°，连接AD、OC、BC，下列结论不正确的是（）

A、EF∥CD B、△COB是等边三角形 C、CG=DG D、的长为 $\frac{3}{2}$ π

查看试题解析
13. 八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（）

A、 $\frac{10}{x} - \frac{10}{2 x} = 20$ B、 $\frac{10}{2 x} - \frac{10}{x} = 20$ C、 $\frac{10}{x} - \frac{10}{2 x} = \frac{1}{3}$ D、 $\frac{10}{2 x} - \frac{10}{x} = \frac{1}{3}$

查看试题解析
14.
如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：
①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若 $\frac{A E}{A B} = \frac{2}{3}$ ，则3S_△_EDH=13S_△_DHC ，其中结论正确的有（）

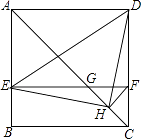A、1个 B、2个 C、3个 D、4个

查看试题解析

三、综合题：

15. 计算：2016⁰﹣|﹣ $\sqrt{2}$ |+ ${(\frac{1}{3})}^{- 1}$ +2sin45°．

查看试题解析
16.
如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB
求证：AE=CE．

查看试题解析
17.
如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；

(2)、请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；

(3)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
18.
某中学为了了解九年级学生体能状况，从九年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级，并依据测试成绩绘制了如下两幅尚不完整的统计图；

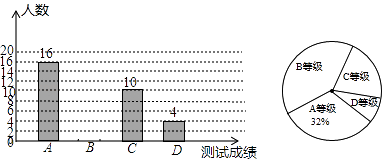(1)、这次抽样调查的样本容量是，并补全条形图；

(2)、D等级学生人数占被调查人数的百分比为，在扇形统计图中C等级所对应的圆心角为°；

(3)、该校九年级学生有1500人，请你估计其中A等级的学生人数．

查看试题解析
19. 甲、乙两个不透明的口袋，甲口袋中装有3个分别标有数字1，2，3的小球，乙口袋中装有2个分别标有数字4，5的小球，它们的形状、大小完全相同，现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字．

(1)、请用列表或树状图的方法（只选其中一种），表示出两次所得数字可能出现的所有结果；

(2)、求出两个数字之和能被3整除的概率．

查看试题解析
20.
如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
21. （列方程（组）及不等式解应用题）
春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．

(1)、求甲、乙两种商品每件的进价分别是多少元？

(2)、商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

查看试题解析
22.
如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．

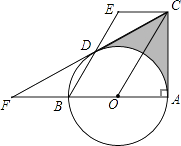(1)、求证：CF是⊙O的切线；

(2)、若∠F=30°，EB=4，求图中阴影部分的面积（结果保留根号和π）

查看试题解析
23.
如图1，对称轴为直线x= $\frac{1}{2}$ 的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A

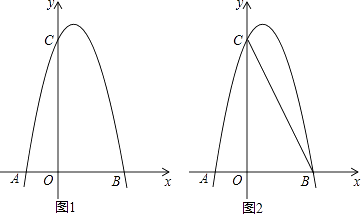(1)、求抛物线的解析式；

(2)、若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；

(3)、如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

人数（人）	1	3	4	1
分数（分）	80	85	90	95