2016年湖北省黄冈市中考数学试卷
试卷更新日期:2016-09-08 类型:中考真卷
一、选择题:
-
1. ﹣2的相反数是( )A、2 B、﹣2 C、- D、2. 下列运算结果正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、a3÷a2=a D、(a2)3=a53.
如图,直线a∥b,∠1=55°,则∠2=( )
 A、35° B、45° C、55° D、65°4. 若方程3x2﹣4x﹣4=0的两个实数根分别为x1 , x2 , 则x1+x2=( )A、﹣4 B、3 C、- D、5. 如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )
A、35° B、45° C、55° D、65°4. 若方程3x2﹣4x﹣4=0的两个实数根分别为x1 , x2 , 则x1+x2=( )A、﹣4 B、3 C、- D、5. 如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )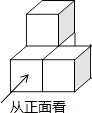 A、
A、 B、
B、 C、
C、 D、
D、 6. 在函数y= 中,自变量x的取值范围是( )A、x>0 B、x≥﹣4 C、x≥﹣4且x≠0 D、x>0且x≠﹣1
6. 在函数y= 中,自变量x的取值范围是( )A、x>0 B、x≥﹣4 C、x≥﹣4且x≠0 D、x>0且x≠﹣1二、填空题:
-
7. 的算术平方根是8. 分解因式:4ax2﹣ay2= .9. 计算:|1﹣ |﹣ = .10. 计算(a﹣ )÷ 的结果是 .11.
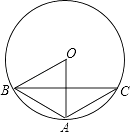
如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC= .
 12. 需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数,现抽取8个排球,通过检测所得数据如下(单位:克):+1,﹣2,+1,0,+2,﹣3,0,+1,则这组数据的方差是 .13.
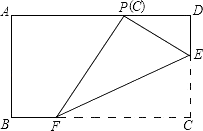
12. 需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数,现抽取8个排球,通过检测所得数据如下(单位:克):+1,﹣2,+1,0,+2,﹣3,0,+1,则这组数据的方差是 .13.如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
 14.
14.如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .

三、解答题:
-
15. 解不等式 .16. 在红城中学举行的“我爱祖国”征文活动中,七年级和八年级共收到征文118篇,且七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇?17.
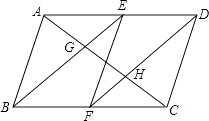
如图,在▱ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
 18. 小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.(1)、请你用画树状图法或列举法,列出所有可能的结果;(2)、求两人再次成为同班同学的概率.19. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
18. 小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.(1)、请你用画树状图法或列举法,列出所有可能的结果;(2)、求两人再次成为同班同学的概率.19. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证: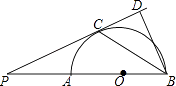 (1)、∠PBC=∠CBD;(2)、BC2=AB•BD.20. 望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)、∠PBC=∠CBD;(2)、BC2=AB•BD.20. 望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: (1)、m=%,n=%,这次共抽查了名学生进行调查统计;(2)、请补全上面的条形图;(3)、如果该校共有1200名学生,请你估计该校C类学生约有多少人?21.
(1)、m=%,n=%,这次共抽查了名学生进行调查统计;(2)、请补全上面的条形图;(3)、如果该校共有1200名学生,请你估计该校C类学生约有多少人?21.如图,已知点A(1,a)是反比例函数y=﹣ 的图象上一点,直线y=﹣ 与反比例函数y=﹣ 的图象在第四象限的交点为点B.
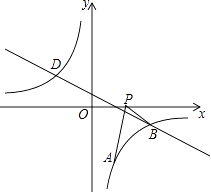 (1)、求直线AB的解析式;(2)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.22.
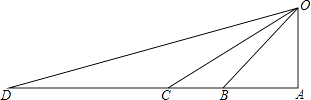
(1)、求直线AB的解析式;(2)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.22.“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45℃D=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据: ≈1.4, ≈1.7).
 23. 东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= 且其日销售量y(kg)与时间t(天)的关系如表:
23. 东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= 且其日销售量y(kg)与时间t(天)的关系如表:时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.24.如图,抛物线y=﹣ 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
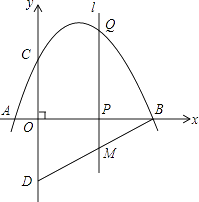 (1)、求点A、点B、点C的坐标;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求点A、点B、点C的坐标;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.