浙江省绍兴市柯桥区校际联盟2017-2018学年七年级上学期数学期中考试试卷

试卷更新日期：2017-11-22 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各数互为相反数的是（）

A、 ${(- 2)}^{3}$ 与 $- 2^{3}$ B、 $3^{2}$ 与 ${(- 3)}^{2}$ C、 $3^{2}$ 与 $- 3^{2}$ D、 $- 3^{2}$ 与 $- {(- 3)}^{2}$

查看试题解析
2. 下列说法正确的是（）

A、 $\sqrt{4}$ 的算术平方根是2 B、互为相反数的两数的立方根也互为相反数 C、平方根是它本身的数有0和1 D、 $\frac{8}{27}$ 的立方根是± $\frac{2}{3}$

查看试题解析
3. 计算 $6 - (+ 3) - (- 7) + (- 5)$ 结果是（）

A、-7 B、-9 C、5 D、-3

查看试题解析
4. 当x=-1时，代数式x²-x+k的值为0，则k的值是（）

A、-2 B、-1 C、0 D、2

查看试题解析
5. 若单项式 $- \frac{2 x^{2} y}{3}$ 的系数是m，次数是n，则mn的值为（）

A、-2 B、-6 C、-4 D、- $\frac{4}{3}$

查看试题解析
6. 下列叙述正确的是（）
①数轴上的点与实数一一对应；
②单项式-πmn的次数是3次；
③若五个数的积为负数，则其中正因数有2个或4个；
④近似数3.70是由 a 四舍五入得到的，则 a 的范围为3.695≤a﹤3.705；
⑤倒数等于本身的数是1

A、①④ B、①②④ C、②④⑤ D、①②③⑤

查看试题解析
7. 运用分配律计算 $13 \frac{5}{7} \times \frac{3}{16}$ 时，下列变形最简便的是（）

A、 $(13 + \frac{5}{7}) \times \frac{3}{16}$ B、 $(14 - \frac{2}{7}) \times \frac{3}{16}$ C、 $(10 + 3 \frac{5}{7}) \times \frac{3}{16}$ D、 $(16 - 2 \frac{2}{7}) \times \frac{3}{16}$

查看试题解析
8. 某城市按以下规定收取每月煤气费，用煤气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费.已知甲用户某月份用煤气80每立方米，那么这个月甲用户应交煤气费（）

A、64元 B、66元 C、72元 D、96元

查看试题解析
9. 如图，长为a ，宽为b的长方形中阴影部分的面积是（）

A、 $\frac{a b}{4}$ B、 $\frac{a b}{2}$ C、ab D、 $\frac{a + b}{2}$

查看试题解析
10. 规定：正整数n的“H运算”是：①当n为奇数时，H=3n+13；②当n为偶数时，H=n $\times \frac{1}{2} \times \frac{1}{2}$ …（连续乘以 $\frac{1}{2}$ ，一直算到H为奇数止）.如：数3经过“H运算”的结果是22，经过2次“H运算”的结果为11，经过三次“H运算”的结果为46，那么257经2017次“H运算”得到的结果是（）

A、161 B、1 C、16 D、以上答案均不正确

查看试题解析

二、填空题

11. 化简： $- 2 (\frac{1}{2} x - y)$ =.

查看试题解析
12. 据统计，全球每分钟有8500000吨污水排入江河湖海，用科学记数法表示为

查看试题解析
13. “早穿皮袄午穿纱”这句民谣形象地描绘了我国新疆奇妙的气温变化现象。乌鲁木齐五月的某一天，最高气温是18℃，温差是20℃，则当天的最低气温是℃

查看试题解析
14. 请写出一个二次多项式，含有两个字母，且常数项是-2..

查看试题解析
15. a是 $\sqrt{10}$ 的整数部分，b的立方根为-2，则a+b的值为。

查看试题解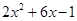析
16. 代数式的值为3，则代数式的值为.

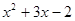查看试题解析
17. 一个三角形一边长为a＋b，另一边比这条边长2a＋b，第三条边比这条边短3a－b，这个三角形的周长为.

查看试题解析
18. 下列图形是将正三角形按一定规律排列，则第4个图形中所有正三角形的个数是.

查看试题解析
19. 如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，那么第二次“移位”后他所处的顶点的编号为. 第181次“移位”后，则他所处顶点的编号是.

查看试题解析

三、解答题

20. 把下列各数填入相应的集合中：
＋2，－3，0，－3 $\frac{1}{2}$ ，－1.414，－17， $\frac{2}{3}$ ．
负数：｛…｝；正整数：｛…｝；
整数：｛…｝；负分数：｛…｝；
分数：｛…｝；有理数：｛…｝．

查看试题解析
21. 计算：

(1)、 $(\frac{2}{3} + \frac{1}{2}) \div (- \frac{1}{12}) \times (- 12)$ .

(2)、 $(\frac{1}{2} + \frac{5}{6} - \frac{7}{12}) \times (- 36)$

(3)、 $- 2^{2} - \sqrt{16} + {(- 1)}^{2017} \times {\frac{1}{11}}^{}$

(4)、 $2 (x^{2} - 3 x^{2} + 1) - 3 (2 x^{2} - x - 2)$

查看试题解析
22. 一辆汽车沿着一条南北方向的公路来回行驶.某一天早晨从A地出发，晚上到达B地.约定向北为正，向南为负，当天记录如下：(单位：千米)－18.3，－9.5，+7.1，－14，－6.2，+13，－6.8，－8.5

(1)、问B地在A地何处，相距多少千米?

(2)、若汽车行驶每千米耗油0.2升，那么这一天共耗油多少升?

查看试题解析
23. 已知M＝x²－2xy＋y² ， N＝2x²－6xy＋3y² ，求3M－[2M－N－4(M－N)]的值，其中x＝－5，y＝3.

查看试题解析
24. 在如图所示的3×3的方格中，画出4个面积小于9的不同的正方形，而且所画正方形的顶点都在方格的顶点上.

查看试题解析
25. 为了加强公民的节水意识，合理利用水资源，某市采取价格调控手段以达到节水的目的，下表是该市自来水收费价格的价目表．
价目表
每月用水量
单价
不超出6 m³的部分
2元/m³
超出6 m³但不超出10 m³的部分
4元/m³
超出10 m³的部分
8元/m³
注：水费按月结算.

(1)、填空：若该户居民2月份用水4 m³ ，则应收水费元；

(2)、若该户居民3月份用水a m³(其中6<a<10)，则应收水费多少元？(用含a的整式表示并化简)

(3)、若该户居民4，5月份共用水15 m³(5月份用水量超过了4月份)，设4月份用水x m³ ，求该户居民4，5月份共交水费多少元？(用含x的整式表示并化简)

查看试题解析
26. 动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A、B的速度比是1：4．（速度单位：单位长度/秒）

(1)、求出两个动点运动的速度；

(2)、若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；

(3)、在（2）中A、B两点继续同时向数轴负方向运动时，另一动点C同时从B点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．

查看试题解析

价目表
每月用水量	单价
不超出6 m³的部分	2元/m³
超出6 m³但不超出10 m³的部分	4元/m³
超出10 m³的部分	8元/m³
注：水费按月结算.