天津市滨海新区2017年中考数学二模试卷

试卷更新日期：2017-11-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算（﹣6）÷（﹣3）的结果是（）

A、 $\frac{1}{2}$ B、2 C、﹣2 D、3

查看试题解析
2. $\frac{1}{2}$ tan60°的值等于（）

A、3 B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）

A、3.12×10⁵ B、3.12×10⁶ C、31.2×10⁵ D、0.312×10⁷

查看试题解析
5. 用3个完全相同的小正方体组合成如图所示的立体图形，它的俯视图为（）

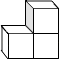A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{7}$ +1的值（）

A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间

查看试题解析
7. 化简 $\frac{x^{2}}{x - 1}$ + $\frac{x}{1 - x}$ 的结果是（）

A、x+2 B、x﹣1 C、﹣x D、x

查看试题解析
8. 一元二次方程x²﹣4x+3=0的根是（）

A、﹣1 B、﹣3 C、1和3 D、﹣1和﹣3

查看试题解析
9. 有理数a、b在数轴上的对应的位置如图所示，则下列各式中正确的是（）

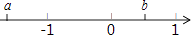A、a+b＜0 B、a+b＞0 C、a﹣b=0 D、a﹣b＞0

查看试题解析
10. 函数y= $\frac{k}{x}$ 的图象经过点（﹣ $\frac{1}{2}$ ，2），则函数y=kx﹣2的图象不经过第几象限（）

A、一 B、二 C、三 D、四

查看试题解析
11. 如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置．此时AC′的中点恰好与点D重合，AB′交CD于点E，若AB=3，则△AEC的面积为（）

A、3 B、 $\frac{3}{2}$ C、2 $\sqrt{3}$ D、 $\sqrt{3}$

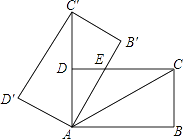查看试题解析
12. 二次函数y=ax²+bx+c（a、b、c为常数，且a≠0）中x与y的部分对应值如表：
x
﹣1
0
1
3
y
﹣1
3
5
3
①ac＜0；
②当x＞1时，y的值随x值的增大而减小；
③x=3是方程ax²+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax²+（b﹣1）x+c＞0．
上述结论中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

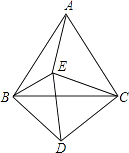
13. 计算（﹣2y³）²的结果等于．

查看试题解析
14. 计算（4 $\sqrt{2}$ ﹣ $\sqrt{8}$ ）÷2 $\sqrt{2}$ 的结果是．

查看试题解析
15. 一个均匀的正六面体的六个面上，有一个面写1，两个面写2，三个面写3，任意投掷一次该六面体，则朝上的一面是3的可能性是．

查看试题解析
16. 一次函数y=（k﹣3）x+2，若y随x的增大而增大，则k的取值范围是．

查看试题解析
17. 如图，设△ABC和△CDE都是等边三角形，且∠EBD=62°，则∠AEB的度数是．

查看试题解析
18. 如图，将放在每个小正方形的边长为1的网格中，点A，B，C均落在格点上．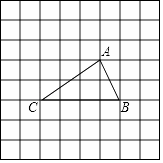

(1)、计算AB边的长等于；

(2)、在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使矩形的面积等于△ABC的面积，并简要说明画图的方法（不要求证明）．

查看试题解析

三、解答题

19. 解不等式组 ${\begin{matrix} 3 x - 2 < 2 x ① \\ \frac{1 + x}{2} - 1 \leq x ② \end{matrix}$ 请结合题意填空，完成本题的解答．
（Ⅰ）解不等式①，得；
（Ⅱ）解不等式②，得；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为．

查看试题解析
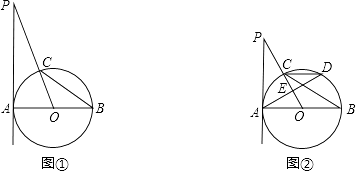
20. 某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：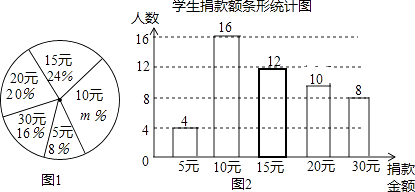

(1)、本次接受随机抽样调查的学生人数为，图①中m的值是；

(2)、求本次你调查获取的样本数据的平均数、众数和中位数；

(3)、根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

查看试题解析
21. 如图，AB是⊙O的直径，PA切⊙O于A，OP交⊙O于C，连接BC．
（Ⅰ）如图①，若∠P=20°，求∠BCO的度数；
（Ⅱ）如图②，过A作弦AD⊥OP于E，连接DC，若OE= $\frac{1}{2}$ CD，求∠P的度数．

查看试题解析
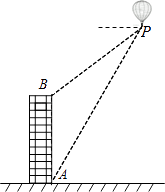
22. 如图，利用热气球探测器测量大楼AB的高度，从热气球P处测得大楼B的俯角为37°，大楼底部A的俯角为60°，此时热气球P离底面的高度为120m．试求大楼AB的高度（结果保留整数）．
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{3}$ ≈1.73）

查看试题解析

23. 某旅行团计划今年暑假组织一个老年人团去昆明旅游，预定宾馆住宿时，有住宿条件一样的甲、乙两家宾馆供选择，其收费标准为某人每天120元，并且各自推出不同的优惠方案：甲家是35人（含35人）以内的按标准收费，超过35人的，超出部分按九折收费；乙家是45人（含45人）以内的按标准收费，超过45人的，超出部分按八折收费．

设老年人团的人数为x

(1)、根据题意，用含x的式子填写下表：

	x≤35	35＜x＜45	x=45	x＞45
甲宾馆收费/元	120x		5280
乙宾馆收费/元	120x	120x	5400

(2)、当老年人团的人数为何值时，在甲、乙两家宾馆的花费相同？如果老年人团的人数超过60人，在哪家宾馆住宿比较省钱？

查看试题解析

24. 将一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，OA=6，OC=10．
（Ⅰ）如图①，在OA上取一点E，将△EOC沿EC折叠，使点O落在AB边上的D点，求E点的坐标；
（Ⅱ）如图②，在OA、OC边上选取适当的点E′、F，将△E′OF沿E′F折叠，使O点落在AB边上D′点，过D′作D′G∥OA交E′F于T点，交OC于G点，设T的坐标为（x，y），求y与x之间的函数关系式，并直接写出自变量x的取值范围；
（Ⅲ）在（Ⅱ）的条件下，若OG=2 $\sqrt{3}$ ，求△D′TF的面积．（直接写出结果即可）

查看试题解析
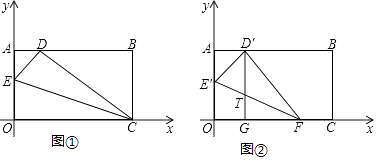25. 已知直线l：y=kx和抛物线C：y=ax²+bx+1．
（Ⅰ）当k=1，b=1时，抛物线C：y=ax²+bx+1的顶点在直线l：y=kx上，求a的值；
（Ⅱ）若把直线l向上平移k²+1个单位长度得到直线r，则无论非零实数k取何值，直线r与抛物线C都只有一个交点；
（i）求此抛物线的解析式；
（ii）若P是此抛物线上任一点，过点P作PQ∥y轴且与直线y=2交于点Q，O为原点，求证：OP=PQ．

查看试题解析

x	﹣1	0	1	3
y	﹣1	3	5	3