四川省绵阳市2017年中考数学二模试卷

试卷更新日期：2017-11-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 如果代数式 $\frac{\sqrt{x - 3}}{x + 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥3且x≠﹣1 B、x＞3且x≠﹣1 C、x＞﹣1 D、x≥3

查看试题解析
2. 若下列选项中的图形均为正多边形，则哪一个图形恰有4条对称轴？（）

A、 B、 C、 D、

查看试题解析
3. 在亚欧商博会重点项目推介会暨签约仪式上，某公司和绵阳市政府正式签署了一个生态农牧产业园项目．该项目计划总投资21.75亿元，计划自2017年起五年内分三期建设，把21.75亿元用科学记数法表示为（）

A、2.175×10⁸元 B、2.175×10⁷元 C、2.175×10⁹元 D、2.175×10⁶元

查看试题解析
4. 将一副常规的三角尺按如图方式放置，则图中∠AOB的度数为（）

A、75° B、95° C、105° D、120°

查看试题解析
5. 下列各式计算正确的是（）

A、m²•m³=m⁶ B、 $\sqrt{16 \frac{1}{3}} = \sqrt{16} \cdot \sqrt{\frac{1}{3}} = \frac{4}{3} \sqrt{3}$ C、 $\sqrt[3]{2^{3} + 3^{3}} = 2 + 3 = 5$ D、 $(a - 1) \sqrt{\frac{1}{1 - a}} = - \sqrt{{(1 - a)}^{2} \cdot \frac{1}{1 - a}} = - \sqrt{1 - a}$ （a＜1）

查看试题解析
6. 由四个相同的小正方体搭建了一个积木，它的三视图如图所示，则这个积木可能是（）

A、 B、 C、 D、

查看试题解析
7. 九年级一班和二班每班选8名同学进行投篮比赛，每名同学投篮10次，对每名同学投中的次数进行统计，甲说：“一班同学投中次数为6个的最多”乙说：“二班同学投中次数最多与最少的相差6个．”上面两名同学的议论能反映出的统计量是（）

A、平均数和众数 B、众数和极差 C、众数和方差 D、中位数和极差

查看试题解析
8. 小张同学去展览馆看展览，该展览馆有2个验票口A、B（可进出），另外还有2个出口C、D（不许进）．小张不从同一个验票口进出的概率是多少（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
9. 某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度约为（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）（）

A、8.1米 B、17.2米 C、19.7米 D、25.5米

查看试题解析
10. 如图，在一个三角点阵中，从上向下数有无数多行，其中各行点数依次为2，4，6，…，2n，…，请你探究出前n行的点数和所满足的规律、若前n行点数和为930，则n=（）

A、29 B、30 C、31 D、32

查看试题解析
11. 如图，将一张边长为3的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，这个棱柱的侧面积为（）

A、9 B、9﹣3 $\sqrt{3}$ C、 $9 - \frac{5}{2} \sqrt{3}$ D、 $9 - \frac{3}{2} \sqrt{3}$

查看试题解析
12. 如图，在正方形ABCD中，点O为对角线AC的中点，过点o作射线OG、ON分别交AB，BC于点E，F，且∠EOF=90°，BO、EF交于点P．则下列结论中：
⑴图形中全等的三角形只有两对；
⑵正方形ABCD的面积等于四边形OEBF面积的4倍；
⑶BE+BF= $\sqrt{2}$ OA；
⑷AE²+CF²=2OP•OB．
正确的结论有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 因式分解：16x⁴﹣4y²= ．

查看试题解析
14. 如图，AB∥CD，∠A=60°，∠C=25°，G、H分别为CF、CE的中点，则∠1=度．

查看试题解析
15. 新定义：[a，b]为一次函数y=ax+b（a≠0，a，b为实数）的“关联数”．若“关联数”[1，m﹣2]的一次函数是正比例函数，则关于x的方程 $\frac{1}{x - 1} + \frac{1}{m} = 1$ 的解为．

查看试题解析
16. 甲乙两地相距50千米．星期天上午8：00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后，小明的父亲骑摩托车沿同一路线也从甲地前往乙地，他们行驶的路程y（千米）与小聪行驶的时间x（小时）之间的函数关系如图所示，小明父亲出发小时时，行进中的两车相距8千米．

查看试题解析
17. 把△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得到△AB′C′，即如图，∠BAB′=θ， $\frac{A B'}{A B}$ = $\frac{B' C'}{B C}$ = $\frac{A C'}{A C}$ =n，我们将这种变换记为[θ，n]．△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，那么θ= ， n= ．

查看试题解析
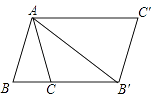18. 二次函数y=ax²﹣bx+b（a＞0，b＞0）图象的顶点的纵坐标不大于 $- \frac{b}{2}$ ，且图象与x轴交于A，B两点，则线段AB长度的最小值是．

查看试题解析

三、解答题

19. 计算题:二次根式与分式运算

(1)、计算：（ $\frac{1}{3}$ ）^﹣²+（ $\sqrt{2010}$ ﹣ $\sqrt{2012}$ ）⁰+（﹣1）¹⁰⁰¹+（ $\sqrt{12}$ ﹣3 $\sqrt{3}$ ）×tan30°

(2)、先化简，再求值： $\frac{1}{2 a}$ ﹣ $\frac{1}{a - b}$ （ $\frac{a - b}{2 a}$ ﹣a²+b²），其中a=3﹣2 $\sqrt{2}$ ，b=3 $\sqrt{2}$ ﹣3．

查看试题解析
20. 为深化义务教育课程改革，满足学生的个性化学习需求，某校就“学生对知识拓展，体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查（每人选报一类），绘制了如图所示的两幅统计图（不完整），请根据图中信息，解答下列问题：

(1)、求扇形统计图中m的值，并补全条形统计图；

(2)、在被调查的学生中，随机抽一人，抽到选“体育特长类”或“艺术特长类”的学生的概率是多少？

(3)、已知该校有800名学生，计划开设“实践活动类”课程每班安排20人，问学校开设多少个“实践活动类”课程的班级比较合理？

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．AO交⊙O于点E，延长AO交⊙O于点D，tanD= $\frac{1}{2}$ ，

(1)、求 $\frac{A E}{A C}$ 的值．

(2)、设⊙O的半径为3，求AB的长．

查看试题解析
22. 如图，已知A是双曲线y= $\frac{k}{x}$ （k＞0）在第一象限内的一点，O为坐标原点，直线OA交双曲线于另一点C，当OA在第一象限的角平分线上时，将OA向上平移 $\frac{3}{2}$ 个单位后，与双曲线在第一象限交于点M，交y轴于点N，若 $\frac{O A}{M N}$ =2，

(1)、求直线MN的解析式；

(2)、求k的值．

查看试题解析
23. 某服装公司招工广告承诺：熟练工人每月工资至少3000元．每天工作8小时，一个月工作25天．月工资底薪800元，另加计件工资．加工1件A型服装计酬16元，加工1件B型服装计酬12元．在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时，加工3件A型服装和1件B型服装需7小时．（工人月工资=底薪+计件工资）

(1)、一名熟练工加工1件A型服装和1件B型服装各需要多少小时？

(2)、一段时间后，公司规定：“每名工人每月必须加工A，B两种型号的服装，且加工A型服装数量不少于B型服装的一半”．设一名熟练工人每月加工A型服装a件，工资总额为W元．请你运用所学知识判断该公司在执行规定后是否违背了广告承诺？

查看试题解析
24. 如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴的正半轴上，点B在第一象限．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA．过点P作PD⊥OB于D点

(1)、直接写出BD的长并求出点C的坐标（用含t的代数式表示）

(2)、在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；

(3)、点P从点O运动到点A时，点C运动路线的长是多少？

查看试题解析
25. 已知在平面直角坐标系xOy中，O为坐标原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，点C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，抛物线y=ax²+bx+c（a≠0）经过点D．

(1)、如图1，若该抛物线经过原点O，且a=﹣ $\frac{1}{3}$ ．
①求点D的坐标及该抛物线的解析式；
②连结CD，问：在抛物线上是否存在点P，使得∠POB与∠BCD互余？若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；

(2)、如图2，若该抛物线y=ax²+bx+c（a≠0）经过点E（1，1），点Q在抛物线上，且满足∠QOB与∠BCD互余．若符合条件的Q点的个数是3个，请直接写出a的值．

查看试题解析