山西省吕梁市孝义市2017年中考数学二模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. 计算﹣3×2的结果等于( )A、﹣1 B、﹣5 C、﹣6 D、12. 估计 的大小在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间3. 如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
 A、40×70×80 B、80×80×40 C、40×40×70 D、70×70×804. 化简 + 的结果是( )A、﹣x﹣y B、y﹣x C、x﹣y D、x+y5. 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
A、40×70×80 B、80×80×40 C、40×40×70 D、70×70×804. 化简 + 的结果是( )A、﹣x﹣y B、y﹣x C、x﹣y D、x+y5. 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( ) A、0.334×10﹣9米 B、3.34×10﹣9米 C、3.34×10﹣10米 D、3.34×10﹣8米6. 某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81.该组数据的中位数是( )A、77.3 B、91 C、81 D、787. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、
A、0.334×10﹣9米 B、3.34×10﹣9米 C、3.34×10﹣10米 D、3.34×10﹣8米6. 某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81.该组数据的中位数是( )A、77.3 B、91 C、81 D、787. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、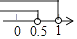 B、
B、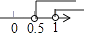 C、
C、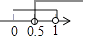 D、
D、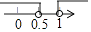 8. 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>﹣1的解集是( )
8. 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>﹣1的解集是( )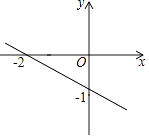 A、x>﹣2 B、x<﹣2 C、x>0 D、x<09. 如图,△ABC与△DEF是位似图形,点A(﹣1,2)和点D(2,﹣4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
A、x>﹣2 B、x<﹣2 C、x>0 D、x<09. 如图,△ABC与△DEF是位似图形,点A(﹣1,2)和点D(2,﹣4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( ) A、(2m,2n) B、(﹣2m,﹣2n) C、(2m,﹣2n) D、(﹣2m,2n)10. 如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
A、(2m,2n) B、(﹣2m,﹣2n) C、(2m,﹣2n) D、(﹣2m,2n)10. 如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( ) A、16 B、16 C、20 D、20
A、16 B、16 C、20 D、20二、填空题
-
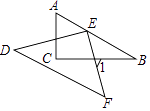
11. 将一副三角尺按如图所示方式摆放,若斜边DF∥AB,则∠1的度数为 .
 12. 某广告公司欲招聘一名创作总监,对2名应试者进行了三项素质测试,他们的各项测试成绩如下表所示:
12. 某广告公司欲招聘一名创作总监,对2名应试者进行了三项素质测试,他们的各项测试成绩如下表所示:应试者
测试成绩
创新能力
计算机能力
公关能力
甲
72
50
88
乙
85
74
45
如果公司赋予“创新能力”、“计算机能力”、“公关能力”三项的权重为5:3:2,则本次招聘中应试者将被录用(填“甲”或“乙”)
13. 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程 . 14. 如图1是一种阳台户外伸缩晾衣架,侧面示意图如图2所示,其支架AB,CD,EF,GH,BE,DG,FK的长度都为40cm(支架的宽度忽略不计),四边形BQCP、DMEQ、FNGM是互相全等的菱形,当晾衣架的A端拉伸到距离墙壁最远时,∠B=∠D=∠F=80°,这时A端到墙壁的距离约为cm.
14. 如图1是一种阳台户外伸缩晾衣架,侧面示意图如图2所示,其支架AB,CD,EF,GH,BE,DG,FK的长度都为40cm(支架的宽度忽略不计),四边形BQCP、DMEQ、FNGM是互相全等的菱形,当晾衣架的A端拉伸到距离墙壁最远时,∠B=∠D=∠F=80°,这时A端到墙壁的距离约为cm.(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)
 15. 如图,点A是反比例函数y= (x>0)的图象上一点,OA与反比例函数y= (x>0)的图象交于点C,点B在y轴的正半轴上,且AB=OA,若△ABC的面积为6,则k的值为 .
15. 如图,点A是反比例函数y= (x>0)的图象上一点,OA与反比例函数y= (x>0)的图象交于点C,点B在y轴的正半轴上,且AB=OA,若△ABC的面积为6,则k的值为 .
三、解答题
-
16. 计算题:计算和分解因式(1)、计算: ﹣|﹣4|+2cos60°﹣(﹣ )﹣1(2)、因式分解:(x﹣y)(x﹣4y)+xy.17. 解方程: = .18. “五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
 19. 如图,△ABC是直角三角形,∠ACB=90°,∠A=30°
19. 如图,△ABC是直角三角形,∠ACB=90°,∠A=30° (1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
(1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).①作△ABC的外接圆O;
②在AB的延长线上作一点D,使得CD与⊙O相切;
(2)、综合与运用:在你所作的图中,若AC=6,则由线段CD,BD及 所围成图形的面积为 .20. 阅读下列材料,完成相应任务:折纸三等分角
三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角.
如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法:
①在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图1;
②翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图2;
③折出射线BQ,BT,得到图3,则射线BQ,BT就是∠SBC的三等分线.

下面是证明BQ,BT是∠SBC三等分线的部分过程:
证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形
根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB
∴△EBT≌△QTB,
∴∠BQT=∠TEB=90°,
∴BQ⊥PT
…
学习任务:
(1)、将剩余部分的证明过程补充完整;(2)、若将图1中的点S与点D重合,重复材料中的操作过程得到图4,请利用图4,直接写出tan15°=(不必化简)21. 近年来,某市坚持绿色发展理念,着力建设生态典范城市,大力开展绿化工程建设.某校“社会实践”小组的同学为了了解该市绿地的发展情况,对市园林局进行了走访调查,获取了如下信息:信息1:2015年的绿地总面积(绿地总面积=森林面积+草场面积)为276km2 , 其中森林面积比上一年增长40%,草地面积比上一年增长20%.
信息2:2014年的绿地总面积为200km2 .

求:
(1)、该市2014年的森林面积和草场面积分别为多少km2?(2)、若该市2016年的绿地总面积为338km2 , 求2014年至2016年该市绿地总面积的年平均增长率为多少?22. 综合与实践在数学活动课上,老师给出如下问题,让同学们展开探究活动:
问题情境:
如图(1),在△ABC中,∠ACB=90°,AC=BC=a,点D为AB上一点(0<AD< AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.

解决问题:
下面是学习小组提出的三个问题,请你解答这些问题:
(1)、“兴趣”小组提出的问题是:求证:AD=EF.(2)、“实践”小组提出的问题是:如图(2),若将△ACD沿AB的垂直平分线对折,得到△BCG,连接EG,则线段EG与EF有怎样的数量关系?请说明理由. (3)、“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长EF与AC交于点H,连接HD,FG.求证:四边形DGFH是矩形.
(3)、“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长EF与AC交于点H,连接HD,FG.求证:四边形DGFH是矩形.提出问题:
(4)、完成上述问题的探究后,老师让同学们结合图(3),提一个与四边形DGFH有关的问题.“智慧”小组提出的问题是:当AD为何值时,四边形DGFH的面积最大?
请你参照智慧小组的做法,再提出一个与四边形DGFH有关的数学问题(提出问题即可,不要求进行解答,但所提问题必须有效)
你提出的问题是:
 23. 如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.
23. 如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.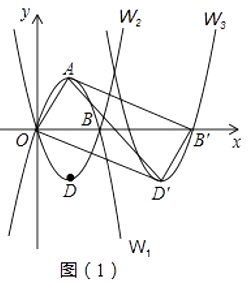 (1)、求抛物线W2的解析式;(2)、将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.(3)、在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
(1)、求抛物线W2的解析式;(2)、将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.(3)、在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
