山东省青岛市市北区2017年中考数学二模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. ﹣5的绝对值为( )A、﹣5 B、5 C、﹣ D、2. 下列图案中,是轴对称图形但不是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. ⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )
3. ⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )
A、相离 B、相切 C、相交 D、重合4. 已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )A、0.000124 B、0.0124 C、﹣0.00124 D、0.001245. 某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是( )
A、90,90 B、90,85 C、90,87.5 D、85,856. 如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm. A、4 B、4π C、8 D、8﹣π7. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、4 B、4π C、8 D、8﹣π7. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、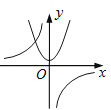 B、
B、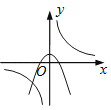 C、
C、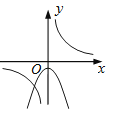 D、
D、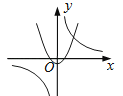 8. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
8. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 = ,则S△EDH=13S△CFH .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 计算:( )﹣1﹣( ﹣ )0= .10. 儿童节期间,游乐场里有一种游戏的规则是:在一个装有6个红球和若干白球(每个球除颜色外,其它都相同)的袋中,随机摸一个球,摸到一个红球就得欢动世界通票一张,已知参加这种游戏的有300人,游乐场为此游戏发放欢动世界通票60张,请你通过计算估计袋中白球的数量是 个.11. 如图,AB是⊙O的直径,AC与⊙O相切于点A,连接OC交⊙O于D,连接BD,若∠C=40°,则∠B=度.
 12. 受季节变化影响,某品牌衬衣经过两次降价,由每件256元降至169元,则平均每次降价的百分率x所满足的方程为 .
12. 受季节变化影响,某品牌衬衣经过两次降价,由每件256元降至169元,则平均每次降价的百分率x所满足的方程为 .
13. 如图,把△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为 . 14. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .
14. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .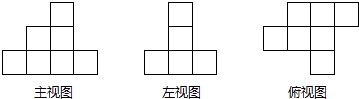
三、作图题
-
15. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图,已知:△ABC中,∠C=90°
求作:矩形CDEF,使点D,E,F分别在边CB,BA,AC上.

四、解答题
-
16. 综合题化简及计算
(1)、化简: ﹣(2)、关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根.求:k的取值范围.17. 为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:组别
成绩x(分)
频数(人数)
频率
一
50≤x<60
2
0.04
二
60≤x<70
10
0.2
三
70≤x<80
14
b
四
80≤x<90
a
0.32
五
90≤x<100
8
0.16
请根据表格提供的信息,解答以下问题:
 (1)、直接写出表中a= , b=;(2)、请补全右面相应的频数分布直方图;(3)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .(4)、请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字)18. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)、直接写出表中a= , b=;(2)、请补全右面相应的频数分布直方图;(3)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .(4)、请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字)18. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.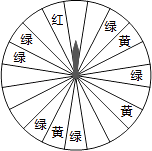 (1)、求转动一次转盘获得购物券的概率;(2)、转转盘和直接获得购物券,你认为哪种方式对顾客更合算?19. 如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)、求转动一次转盘获得购物券的概率;(2)、转转盘和直接获得购物券,你认为哪种方式对顾客更合算?19. 如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°. (1)、求这座山的高度(小明的身高忽略不计);(2)、求索道AC的长(结果精确到0.1m).
(1)、求这座山的高度(小明的身高忽略不计);(2)、求索道AC的长(结果精确到0.1m).(参考数据:tan31°≈ ,sin31°≈ ,tan39°≈ ,sin39°≈ )
20. 东营市某学校2015年在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.(1)、求购买一个甲种足球、一个乙种足球各需多少元;(2)、2016年为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?21. 如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点. (1)、求证:△BOC≌△EOD;(2)、当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.22. 汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
(1)、求证:△BOC≌△EOD;(2)、当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.22. 汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:x(元)
3000
3200
3500
4000
y(辆)
100
96
90
80
(1)、观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.(2)、已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:租出的车辆数(辆)
未租出的车辆数(辆)
租出每辆车的月收益(元)
所有未租出的车辆每月的维护费(元)
(3)、若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.23. 定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. (1)、已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=;(2)、如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(1)、已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=;(2)、如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点; (3)、如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN , S△APB , S△MBH的数量关系.
(3)、如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN , S△APB , S△MBH的数量关系.S△ACN=;S△MBH=;S△APB=;
S△ACN , S△APB , S△MBH的数量关系是 .
 24. 如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.
24. 如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒. (1)、若当t的值为m时,PP′恰好经过点A,求m的值.(2)、设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4)(3)、是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
(1)、若当t的值为m时,PP′恰好经过点A,求m的值.(2)、设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4)(3)、是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
-