山东省滨州市无棣县2017年中考数学二模试卷

试卷更新日期：2017-11-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图所示，用直尺度量线段AB，可以读出AB的长度为（）

A、6cm B、7cm C、8cm D、9cm

查看试题解析
2. 实数a，b，c，d在数轴上的对应点的位置如图所示，则这四个数中，相反数是正数的为（）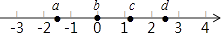

A、a B、b C、c D、d

查看试题解析
3. 下列各式计算正确的是（）

A、a+3a²=3a³ B、（a﹣b）²=a²﹣ab+b² C、2（a﹣b）=2a﹣2b D、（2ab）²÷ab=2ab

查看试题解析
4. 用5个完全相同的小正方体组合成如图所示的立体图形，它的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 今年我市2017年初中毕业生学业考试10门学科整合后的满分值如表：
科目
语文
数学
英语
理化生
政史地
体育
信息技术
实验操作
满分值
120
120
120
150
150
50
20
20
请问数据120，120，120，150，150，50，20，20中，众数、中位数分别是（）

A、150，120 B、120，120 C、130，120 D、120，100

查看试题解析
6. 一次函数y=﹣3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C；直线DF分别交l₁ ， l₂ ， l₃于点D，E，F．AC与DF相交于点H，且AH=2，HB=1，BC=5，则 $\frac{D E}{E F}$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
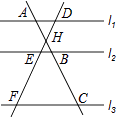8. 如图，在△ABC中，∠BAC=90°，AB=AC=3，点D在BC上且BD=2CD，E，F分别在AB，AC上运动且始终保持∠EDF=45°，设BE=x，CF=y，则y与x之间的函数关系用图象表示为：（）

A、 B、 C、 D、

查看试题解析
9. 若将30°、45°、60°的三角函数值填入表中，则从表中任意取一个值，是 $\frac{\sqrt{2}}{2}$ 的概率为（）
α
30°
45°
60°
sinα

cosα

tanα

A、 $\frac{1}{3}$ B、 $\frac{1}{9}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
10. 如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于点E，则sin∠E的值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
11. 如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，x=﹣1是对称轴，有下列判断：
①b﹣2a=0；②4a﹣2b+c＜0；③a﹣b+c=﹣9a；④若（﹣3，y₁），（ $\frac{3}{2}$ ，y₂）是抛物线上两点，则y₁＞y₂ ，其中正确的是（）

A、①②③ B、①③④ C、①②④ D、②③④

查看试题解析

二、填空题

12. “十三五”开局之年，我市财政总收入达到58400000000元，将这个数用科学记数法表示为．

查看试题解析
13. 分解因式：2a²﹣4a+2= ．

查看试题解析
14. 已知扇形的圆心角为120°，弧长为6π，则它的半径为．

查看试题解析
15. 目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现：小琼步行13500步与小刚步行9000步消耗的能量相同，若每消耗1千卡能量小琼行走的步数比小刚多15步，求小刚每消耗1千卡能量需要行走步．

查看试题解析
16. 已知点A（1，5），B（4，2），点P在x轴上，当PA﹣PB最大时，点P的坐标为．

查看试题解析
17. 规定：log_ab（a＞0，a≠1，b＞0）表示a，b之间的一种运算．
现有如下的运算法则：log_aaⁿ=n．log_NM= $\frac{l o g_{n} M}{l o g_{n} N}$ （a＞0，a≠1，N＞0，N≠1，M＞0）．
例如：log₂2³=3，log₂5= $\frac{l o g_{10} 5}{l o g_{10} 2}$ ，则log₁₀₀1000= ．

查看试题解析

三、解答题

18. 先化简，再求值： $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ÷ $\frac{a + 1}{a - 1}$ ﹣ $\frac{a}{a + 1}$ ，其中a= $\sqrt{2}$ ﹣1．

查看试题解析
19. 如图，在△ABC中，AB=AC，D是边BC上一点，DE⊥AB，DF⊥AC，垂足分别是E，F，△AEF∽△ABC．

(1)、求证：△AED≌△AFD；

(2)、若BC=2AD，求证：四边形AEDF是正方形．

查看试题解析
20. 如图，Rt△ABC中，∠ABC为直角，以AB为直径作⊙O交AC于点D，点E为BC中点，连结DE，DB

(1)、求证：DE与⊙O相切；

(2)、若∠C=30°，求∠BOD的度数；

(3)、在（2）的条件下，若⊙O半径为2，求阴影部分面积．

查看试题解析
21. 如图，一次函数y=ax+b（a≠0）的图形与反比例函数y= $\frac{k}{x}$ （k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= $\frac{4}{3}$ ，点B的坐标为（m，﹣2）．

(1)、求该反比例函数和一次函数的解析式．

(2)、求△AOC的面积．

查看试题解析
22. 为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．王宏按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+400．

(1)、王宏在开始创业的第一个月将销售单价定为18元，那么政府这个月为他承担的总差价为多少元？

(2)、设王宏获得的利润为W（元），当销售单价为多少元时，每月可获得最大利润？

(3)、若物价部门规定，这种节能灯销售单价不得高于24元．如果王宏想要每月获得的利润不低于2000元，那么政府为他承担的总差价最少为多少元？

查看试题解析
23. 如图1（注：与图2完全相同），二次函数y= $\frac{4}{3}$ x²+bx+c的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C．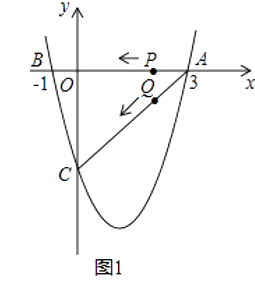

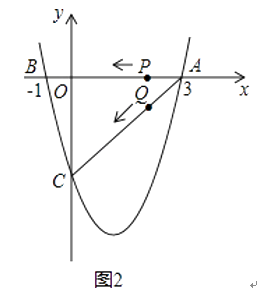(1)、求该二次函数的解析式；

(2)、设该抛物线的顶点为D，求△ACD的面积（请在图1中探索）；

(3)、若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上E点处，请直接判定此时四边形APEQ的形状，并求出E点坐标（请在图2中探索）．

查看试题解析

科目	语文	数学	英语	理化生	政史地	体育	信息技术	实验操作
满分值	120	120	120	150	150	50	20	20

α	30°	45°	60°
sinα
cosα
tanα