内蒙古乌兰察布市集宁七中2017年中考数学一模试卷

试卷更新日期：2017-11-21 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、x²+y²=（x+y）² C、a³•a²=a⁵ D、a³•a²=a⁶

查看试题解析
3. PM2.5是指大气中直径≤0.0000025米的颗粒物，将0.0000025用科学记数法表示为（）

A、2.5×10^﹣⁷ B、2.5×10^﹣⁶ C、25×10^﹣⁷ D、0.25×10^﹣⁵

查看试题解析
4. 函数 $y = \sqrt{2 - x} + \frac{1}{x - 3}$ 中自变量x的取值范围是（）

A、x≤2 B、x=3 C、x＜2且x≠3 D、x≤2且x≠3

查看试题解析
5. 为了解某小区家庭使用垃圾袋的情况，小亮随机调查了该小区10户家庭一周垃圾袋的使用量，结果如下：7，9，11，8，7，14，10，8，9，7（单位：个），关于这组数据下列结论正确的是（　　）

A、极差是6 B、众数是7 C、中位数是8 D、平均数是10

查看试题解析
6. 一个袋子中装有3个红球和2个黄球，这些球的形状、大小．质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{1}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
7. 将一个半径为R，圆心角为90°的扇形围成一个圆锥的侧面（无重叠），设圆锥底面半径为r，则R与r的关系正确的是（）

A、R=8r B、R=6r C、R=4r D、R=2r

查看试题解析
8. 关于x的一元二次方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤﹣ $\frac{9}{4}$ B、k≤﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k≥﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
9. 如图，平行四边形ABCD的对角线交于点O，且AB≠AD，过O作OE⊥BD交BD于点E．若△CDE的周长为10，则平行四边形ABCD的周长为（）

A、10 B、16 C、18 D、20

查看试题解析
10. 已知下列命题：
①若a＞0，b＞0，则a+b＞0；
②若a²=b² ，则a=b；
③线段垂直平分线上的点到线段两端点距离相等；
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是（）

A、①③ B、②④ C、③④ D、②③

查看试题解析
11. 如图，在正方形ABCD中，对角线AC，BD交于点O，折叠正方形ABCD，使AB边落在AC上，点B落在点H处，折痕AE分别交BC于点E，交BO于点F，连结FH，则下列结论正确的有几个（）
⑴AD=DF；（2） $\frac{S_{△ A B E}}{S △ A C E}$ = $\frac{A B}{A C}$ ；（3） $\frac{F H}{A D}$ = $\sqrt{2}$ ﹣1；（4）四边形BEHF为菱形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①b＜0；②4a+2b+c＜0；③a﹣b+c＞0；④（a+c）²＜b² ．其中正确的结论是（）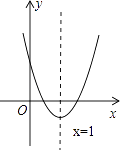

A、①② B、①③ C、①③④ D、①②③④

查看试题解析

二、填空题

13. 计算： $\sqrt{12}$ ﹣2tan60°+（ $\sqrt{2017}$ ﹣1）⁰﹣（ $\frac{1}{3}$ ）^﹣¹= ．

查看试题解析
14. 化简：（ $\frac{x - 1}{x^{2} - 1}$ + $\frac{1}{x + 1}$ ）÷ $\frac{4}{x^{2} + x}$ = ．

查看试题解析
15. 若不等式组 ${\begin{matrix} 2 x - a < 1 \\ x - 2 b > 3 \end{matrix}$ 的解集为﹣1＜x＜1，那么（a+1）（b﹣1）的值等于．

查看试题解析
16. 一组数据5，2，3，6，4，这组数据的方差是．

查看试题解析
17. 如图，AD和AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AD交AC于点B，若OB=5，则BC等于．

查看试题解析
18. 已知点A（﹣2，y₁），B（﹣1，y₂）和C（3，y₃）都在反比例函数y= $\frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系为．（用“＜”连接）

查看试题解析
19. 如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形EBF的半径为2，圆心角为60°，则图中阴影部分的面积是．

查看试题解析
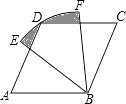20. 如图，已知△ABC是等边三角形，点D，E分别在边BC，AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：
①△ABE≌△ACF；②BC=DF；③S_△_ABC=S_△_ACF+S_△_DCF；④若BD=2DC，则GF=2EG．其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、解答题

21. 如图，有A，B两个转盘，其中转盘A被分成4等份，转盘B被分成3等份，并在每一份内标上数字．现甲、乙两人同时各转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将A转盘指针指向的数字记为x，B转盘指针指向的数字记为y，从而确定点P的坐标为P（x，y）．

(1)、请用列表或画树状图的方法写出所有可能得到的点P的坐标；

(2)、计算点P在函数y= $\frac{6}{x}$ 图象上的概率．

查看试题解析
22. 如图，广安市防洪指挥部发现渠江边一处长400米，高8米，背水坡的坡角为45°的防洪大堤（横截面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽2米，加固后，背水坡EF的坡比i=1：2．

(1)、求加固后坝底增加的宽度AF的长；

(2)、求完成这项工程需要土石多少立方米？

查看试题解析
23. 我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．

(1)、试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；

(2)、当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？

查看试题解析
24. 已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

(1)、求证：点D是AB的中点；

(2)、判断DE与⊙O的位置关系，并证明你的结论；

(3)、若⊙O的直径为18，cosB= $\frac{1}{3}$ ，求DE的长．

查看试题解析
25. 如图，在△ABC中，AB=AC=10cm，BD⊥AC于点D，且BD=8cm．点M从点A出发，沿AC的方向匀速运动，速度为2cm/秒；同时直线PQ由点B出发，沿BA的方向匀速运动，速度为1cm/秒，运动过程中始终保持PQ∥AC，直线PQ交AB于点P、交BC于点Q、交BD于点F．连接PM，设运动时间为t秒（0＜t＜5）．

(1)、当t为何值时，四边形PQCM是平行四边形？

(2)、设四边形PQCM的面积为y（cm²），求y与t之间的函数关系式．

查看试题解析
26. 如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax²﹣10ax+c经过点C，顶点M在直线BC上．

(1)、证明四边形ABCD是菱形，并求点D的坐标；

(2)、求抛物线的对称轴和函数表达式；

(3)、在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析