辽宁省丹东九中2017年中考数学二模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、0 B、 C、﹣3 D、﹣22. 习近平总书记提出了未来5年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×106 B、1.17×107 C、1.17×108 D、11.7×1063. 在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )
 A、全 B、国 C、明 D、城4. 为响应习总书记的足球进校园的号召,我校购进大小两种型号的足球,5个大足球和4个小足球共148元;2个大足球,5个小足球共100元.设大足球每个x元,小足球每个小y元,则可列方程组( )A、 B、 C、 D、5. 一组数据8,3,8,6,7,8,7的众数和极差分别是( )A、8,3 B、8,5 C、7,8 D、8,76. 下列运算正确的是( )A、3a﹣a=2 B、a•a2=a3 C、a6÷a3=a2 D、(a3)2=a57. 如图,已知a∥b,∠1=50°,则∠2=( )
A、全 B、国 C、明 D、城4. 为响应习总书记的足球进校园的号召,我校购进大小两种型号的足球,5个大足球和4个小足球共148元;2个大足球,5个小足球共100元.设大足球每个x元,小足球每个小y元,则可列方程组( )A、 B、 C、 D、5. 一组数据8,3,8,6,7,8,7的众数和极差分别是( )A、8,3 B、8,5 C、7,8 D、8,76. 下列运算正确的是( )A、3a﹣a=2 B、a•a2=a3 C、a6÷a3=a2 D、(a3)2=a57. 如图,已知a∥b,∠1=50°,则∠2=( )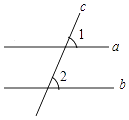 A、40° B、50° C、130° D、140°8. 如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A、40° B、50° C、130° D、140°8. 如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )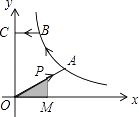 A、
A、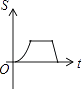 B、
B、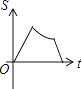 C、
C、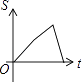 D、
D、
二、填空题
-
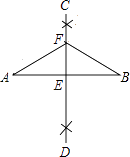
9. 分解因式:x3﹣9x= .10. 不等式组 的解集是 .11. 如图,已知线段AB,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于C,D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB= .
 12. 如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α= .
12. 如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α= .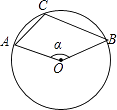 13. 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为 .
13. 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为 .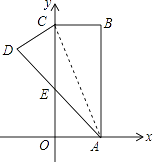 14. 某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .15. 不透明的袋子里装有2个白球,1个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸出白球的概率是 .16. 如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 .
14. 某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .15. 不透明的袋子里装有2个白球,1个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸出白球的概率是 .16. 如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 .
三、解答题
-
17. 计算:( )0+(﹣1)2016﹣|﹣ |+2sin60°.18. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
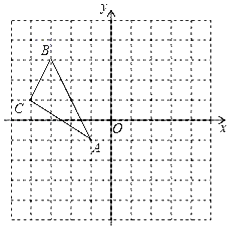
①画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
②画出△ABC向下平移3个单位的△A2B2C2 , 并写出点C的对应点C2的坐标.
四、解答题
-
19. 为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题
 (1)、本次抽样调查共抽取多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(1)、本次抽样调查共抽取多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)、若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)、请你对“不及格”等级的同学提一个友善的建议(一句话即可).五、解答题
-
20. 丹东市政府今春计划维修站前十纬路等工程,拟招标甲乙两个施工队,已知甲队修500米与乙队修路800米所用天数相同,乙队比甲队每天多修30米,问甲队每天修路多少米?
21. 如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.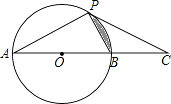 (1)、求证:CP是⊙O的切线.(2)、若⊙O的直径为8,求阴影部分的面积.
(1)、求证:CP是⊙O的切线.(2)、若⊙O的直径为8,求阴影部分的面积.六、解答题
-
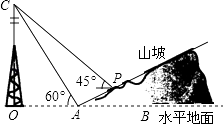
22. 如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为 (即tan∠PAB= ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
 23. 春节前夕,丹东一海鲜批发商以40元/千克的价格购入了某海鲜产品500千克.刚开始准备以60元/千克的价格向外批发,据市场预测,该种海鲜产品批发价每隔一天批发价就涨价2元,但保存这批海鲜产品平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批海鲜产品每天还需40元的费用.(1)、若批发商保存1天后将该批海鲜产品一次性卖出,则卖出时海鲜产品的售价为(元/千克),获得的总利润为(元);(2)、设批发商将这批海鲜产品保存x天后一次性卖出,试求批发商所获得的总利润y(元)与保存时间x(天)之间的函数关系式;并求在哪一天一次性卖出全部海鲜能获得的最大利润及最大利润那是多少.
23. 春节前夕,丹东一海鲜批发商以40元/千克的价格购入了某海鲜产品500千克.刚开始准备以60元/千克的价格向外批发,据市场预测,该种海鲜产品批发价每隔一天批发价就涨价2元,但保存这批海鲜产品平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批海鲜产品每天还需40元的费用.(1)、若批发商保存1天后将该批海鲜产品一次性卖出,则卖出时海鲜产品的售价为(元/千克),获得的总利润为(元);(2)、设批发商将这批海鲜产品保存x天后一次性卖出,试求批发商所获得的总利润y(元)与保存时间x(天)之间的函数关系式;并求在哪一天一次性卖出全部海鲜能获得的最大利润及最大利润那是多少.七、解答题
-
24. 现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC,CD交于点M、N.(1)、如图1,若点O与点A重合,则OM与ON的数量关系是;
 (2)、如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(2)、如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;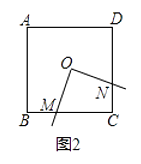 (3)、如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(3)、如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?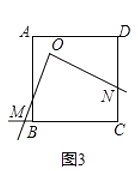 (4)、如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
(4)、如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)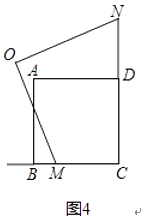
八、解答题
-
25. 已知如图抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C(0,﹣3)
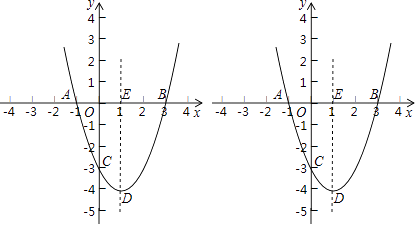 (1)、请直接写出抛物线的解析式.
(1)、请直接写出抛物线的解析式.
(2)、抛物线的对称轴上是否存在一点P,使得△ACP的周长最短,若存在,请直接写出点P的坐标.
(3)、点G的坐标是(2,﹣3),点F是x轴上一点,抛物线上是否存在点R,使得以A,G,F,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标.
(4)、在B、C连线的下方抛物线上是否存在一点Q,使得△QBC的面积是△ABC的面积的一半?若存在,求出点Q的坐标.
(5)、抛物线的顶点设为D,对称轴与y轴的交点为E,M(m,0)是x轴上一动点,点N是线段DE上的一点,若∠MNC=90°,请直接写出实数m的变化范围.
-
-