江苏省泰州市靖江三中2017年中考数学二模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、解答题
-
1. 在下列实数中,无理数是( )
A、2 B、0 C、 D、2. 如图,由两个相同的正方体和一个圆锥体组成一个立体图形,其俯视图是( ) A、
A、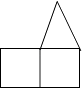 B、
B、 C、
C、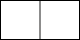 D、
D、 3. 矩形具有而菱形不一定具有的性质是( )A、对边分别相等 B、对角分别相等 C、对角线互相平分 D、对角线相等4. 如图,AB∥EF,CD⊥EF,∠ACD=130°,则∠BAC=( )
3. 矩形具有而菱形不一定具有的性质是( )A、对边分别相等 B、对角分别相等 C、对角线互相平分 D、对角线相等4. 如图,AB∥EF,CD⊥EF,∠ACD=130°,则∠BAC=( )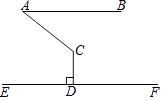 A、40° B、50° C、60° D、70°5. ⊙O的半径为4,圆心到点P的距离为d,且d是方程x2﹣2x﹣8=0的根,则点P与⊙O的位置关系是( )
A、40° B、50° C、60° D、70°5. ⊙O的半径为4,圆心到点P的距离为d,且d是方程x2﹣2x﹣8=0的根,则点P与⊙O的位置关系是( )
A、点P在⊙O内部 B、点P在⊙O上 C、点P在⊙O外部 D、点P不在⊙O上6. 已知关于x的二次函数y=x2+(1﹣a)x+1,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A、a=5 B、a≥5 C、a=3 D、a≥3二、填空题
-
7. 钓鱼诸岛是中国的固有领土,位于中国东海,面积约6344000平方米,数据6344000用科学记数法表示为 .8. 分解因式:2a2﹣8b2=9. 若二次根式 有意义,则x的取值范围是 .10. 已知m,n是方程x2+2x﹣5=0的两个实数根,则m2﹣mn+3m+n= .11. 如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E= .
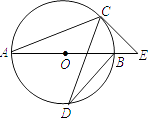 12. 在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是 .
12. 在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是 .
13. 已知扇形的半径为3cm,圆心角为120°,用它做成一个圆锥的侧面,则该圆锥的底面圆的半径是cm.
14. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,3 ),反比例函数y= 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 .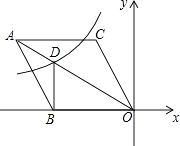 15. 如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为 .
15. 如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为 .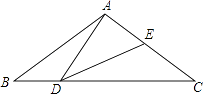 16. 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
16. 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
三、解答题
-
17. 计算题计算:(﹣2017)0+|1﹣ |﹣2cos45°+(﹣ )﹣2;
(1)、计算:(﹣2017)0+|1﹣ |﹣2cos45°+(﹣ )﹣2;
(2)、解不等式组: .
18. 先化简: ,并从0,﹣1,2中选一个合适的数作为a的值代入求值.
19. 西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.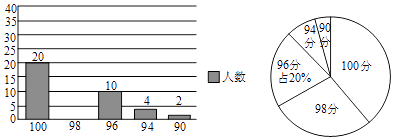
试根据统计图中提供的数据,回答下面问题:
(1)、计算样本中,成绩为98分的学生有分,并补全条形统计图.(2)、样本中,测试成绩的中位数是分,众数是分.(3)、若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合速度测试将有多少名学生可以获得满分.20. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.21. 高考英语听力测试期间,需要杜绝考点周围的噪音.如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队.在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.( 取1.732)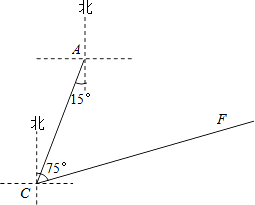 22. 如图,在▱ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
22. 如图,在▱ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.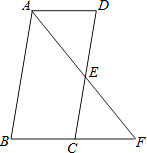 (1)、求证:△ADE和△CEF的面积相等;(2)、若AB=2AD,试说明AF恰好是∠BAD的平分线.23. 如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题:
(1)、求证:△ADE和△CEF的面积相等;(2)、若AB=2AD,试说明AF恰好是∠BAD的平分线.23. 如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题: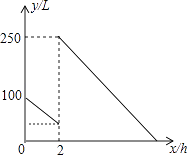 (1)、汽车行驶h后加油,中途加油L;(2)、求加油前油箱剩余油量y与行驶时间x的函数解析式;
(1)、汽车行驶h后加油,中途加油L;(2)、求加油前油箱剩余油量y与行驶时间x的函数解析式;
(3)、若当油箱中剩余油量为10L时,油量表报警,提示需要加油,大巴车不再继续行驶,则该车最远能跑多远?此时,大巴车从出发到现在已经跑了多长时间?
24. 如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.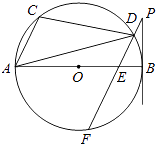 (1)、判断直线BP和⊙O的位置关系,并说明你的理由;(2)、当⊙O的半径为 ,AC=2,BE=1时,求BP的长.25. 我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.(1)、试举出一个有内心的四边形.(2)、如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.
(1)、判断直线BP和⊙O的位置关系,并说明你的理由;(2)、当⊙O的半径为 ,AC=2,BE=1时,求BP的长.25. 我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.(1)、试举出一个有内心的四边形.(2)、如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.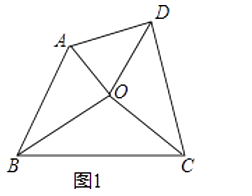 (3)、如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC,BC于点D,E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.
(3)、如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC,BC于点D,E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.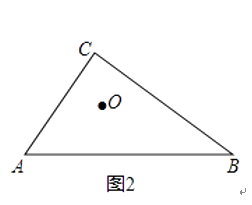 (4)、问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长.26. 如图所示,动点A,B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA,OB为邻边建立正方形OACB,抛物线y=﹣x2+bx+c经过B,C两点,假设A,B两点运动的时间为t秒:
(4)、问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长.26. 如图所示,动点A,B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA,OB为邻边建立正方形OACB,抛物线y=﹣x2+bx+c经过B,C两点,假设A,B两点运动的时间为t秒: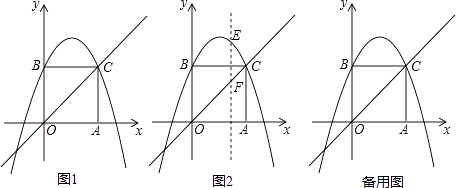 根据(1)、直接写出直线OC的解析式;
根据(1)、直接写出直线OC的解析式;
(2)、当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;(3)、在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)、在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP= ,CP=2,∠OPA=135°,直接写出此时AP的长度.