湖北省襄阳市枣阳市2017年中考数学模拟试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、5 B、﹣3 C、0 D、22. 下列计算正确的是( )A、3x2﹣2x2=1 B、x+x=x2 C、4x8÷2x2=2x4 D、x•x=x23. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
 A、65° B、115° C、125° D、130°4. 长方体的主视图、俯视图如图所示,则其左视图面积为( )
A、65° B、115° C、125° D、130°4. 长方体的主视图、俯视图如图所示,则其左视图面积为( ) A、3 B、4 C、12 D、165. 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
A、3 B、4 C、12 D、165. 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( ) A、2 B、 C、 D、6. 对于非零实数a、b,规定a⊗b= .若2⊗(2x﹣1)=1,则x的值为( )A、 B、 C、 D、﹣7. 在平面直角坐标系中,点P(﹣4,2)向右平移7个单位长度得到点P1 , 点P1绕原点逆时针旋转90°得到点P2 , 则点P2的坐标是( )A、(﹣2,3) B、(﹣3,2) C、(2,﹣3) D、(3,﹣2)8. 小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是( )A、掷一次骰子,在骰子向上的一面上的点数大于0 B、掷一次骰子,在骰子向上的一面上的点数为7 C、掷三次骰子,在骰子向上的一面上的点数之和刚好为18 D、掷两次骰子,在骰子向上的一面上的点数之积刚好是119. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A、2 B、 C、 D、6. 对于非零实数a、b,规定a⊗b= .若2⊗(2x﹣1)=1,则x的值为( )A、 B、 C、 D、﹣7. 在平面直角坐标系中,点P(﹣4,2)向右平移7个单位长度得到点P1 , 点P1绕原点逆时针旋转90°得到点P2 , 则点P2的坐标是( )A、(﹣2,3) B、(﹣3,2) C、(2,﹣3) D、(3,﹣2)8. 小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是( )A、掷一次骰子,在骰子向上的一面上的点数大于0 B、掷一次骰子,在骰子向上的一面上的点数为7 C、掷三次骰子,在骰子向上的一面上的点数之和刚好为18 D、掷两次骰子,在骰子向上的一面上的点数之积刚好是119. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( ) A、128° B、126° C、122° D、120°10. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )
A、128° B、126° C、122° D、120°10. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )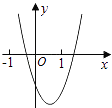 A、
A、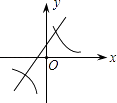 B、
B、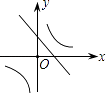 C、
C、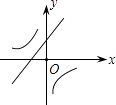 D、
D、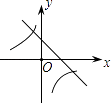
二、填空题
-
11. 计算:(﹣2)0﹣ +2﹣1= .12. 若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x= .13. 已知不等式组: ,其解集为 .14. 如图,在△ABC中,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为 .
 15. 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2 ,则S阴影= .
15. 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2 ,则S阴影= . 16. 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .
16. 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .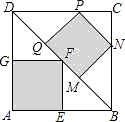
三、解答题
-
17. 先化简,再求值:( +2﹣x)÷ ,其中x满足x2+2x﹣3=0.18. 为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:
 (1)、在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 . 扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.(2)、请你补全条形统计图.(3)、若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.19. 如图,在▱ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.
(1)、在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 . 扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.(2)、请你补全条形统计图.(3)、若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.19. 如图,在▱ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH. 20. 如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
20. 如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽. 21. 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y= (x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
21. 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y= (x>0,k是常数)的图象经过AB边的中点D,交OB边于点E. (1)、求直线OB的函数解析式;(2)、求k的值;(3)、若函数y= 的图象与△DEB没有交点,请直接写出m的取值范围.22. 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)、求直线OB的函数解析式;(2)、求k的值;(3)、若函数y= 的图象与△DEB没有交点,请直接写出m的取值范围.22. 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P. (1)、说明:AP是⊙O的切线;(2)、若OC=CP,AB=6,求CD的长.23. 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ,tan ,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)、说明:AP是⊙O的切线;(2)、若OC=CP,AB=6,求CD的长.23. 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ,tan ,以O为原点,OA所在直线为x轴建立直角坐标系. (1)、求点P的坐标;(2)、水面上升1m,水面宽多少( 取1.41,结果精确到0.1m)?24. 在△ABC中,∠A=90°,点D在线段BC上,∠EDB= ∠C,BE⊥DE,垂足E,DE与AB相交于点F.(1)、当AB=AC时,(如图1),
(1)、求点P的坐标;(2)、水面上升1m,水面宽多少( 取1.41,结果精确到0.1m)?24. 在△ABC中,∠A=90°,点D在线段BC上,∠EDB= ∠C,BE⊥DE,垂足E,DE与AB相交于点F.(1)、当AB=AC时,(如图1),
① ∠EBF=°;
②求证:BE= 1 2 FD;(2)、当AB=kAC时(如图2),求 的值(用含k的式子表示). 25. 已知:如图,在平面直角坐标系xOy中,抛物线 过点A(6,0)和点B(3, ).
25. 已知:如图,在平面直角坐标系xOy中,抛物线 过点A(6,0)和点B(3, ). (1)、求抛物线y1的解析式;
(1)、求抛物线y1的解析式;
(2)、将抛物线y1沿x轴翻折得抛物线y2 , 求抛物线y2的解析式;
(3)、在(2)的条件下,抛物线y2上是否存在点M,使△OAM与△AOB相似?如果存在,求出点M的坐标;如果不存在,说明理由.