湖北省武汉二十四中2017年中考数学模拟试卷

试卷更新日期：2017-11-21 类型：中考模拟

进入出卷网下载

一、选择题：

1. 若a、b、c都是有理数，那么2a﹣3b+c的相反数是（）

A、3b﹣2a﹣c B、﹣3b﹣2a+c C、3b﹣2a+c D、3b+2a﹣c

查看试题解析
2. 若把分式 $\frac{x + y}{2 x y}$ 中的x和y都扩大3倍，且x+y≠0，那么分式的值（）

A、扩大3倍 B、不变 C、缩小3倍 D、缩小6倍

查看试题解析
3. 下列各式中，能用平方差公式计算的是（）

A、 $(a - \frac{1}{2} b) (a - \frac{1}{2} b)$ B、 $(a - \frac{1}{2} b) (- a + \frac{1}{2} b)$ C、 $(- a - \frac{1}{2} b) (a - \frac{1}{2} b)$ D、 $(- a - \frac{1}{2} b) (a + \frac{1}{2} b)$

查看试题解析
4. 下列事件中是不可能事件的是（）

A、降雨时水位上升 B、在南极点找到东西方向 C、体育运动时消耗卡路里 D、体育运动中肌肉拉伤

查看试题解析
5. 下列关于x的方程：
①ax²+bx+c=0；②3（x﹣9）²﹣（x+1）²=1；③x+3= $\frac{1}{x}$ ；④（a²+1）x²﹣a=0；⑤ $\sqrt{x + 1}$ =x﹣1，
其中一元二次方程的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（）

A、（﹣2，﹣1） B、（﹣1，0） C、（﹣1，﹣1） D、（﹣2，0）

查看试题解析
7. 如图，水杯的俯视图是（）

A、 B、 C、 D、

查看试题解析
8. 在2016年我县中小学经典诵读比赛中，10个参赛单位成绩统计如图所示，对于这10个参赛单位的成绩，下列说法中错误的是（）

A、众数是90 B、平均数是90 C、中位数是90 D、极差是15

查看试题解析
9. 如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（）

A、68° B、88° C、90° D、112°

查看试题解析
10. 如图，正方形ABCD和CEFG的边长分别为m、n，那么△AEG的面积的值（）

A、与m、n的大小都有关 B、与m、n的大小都无关 C、只与m的大小有关 D、只与n的大小有关

查看试题解析

二、填空题：

11. 某地某天的最高气温为﹣2℃，最低气温为﹣8℃，这天的温差是℃．

查看试题解析
12. 据统计，全球每分钟约有8500000吨污水排入江河湖海，将8500000用科学记数法表示为吨．

查看试题解析
13. 从数﹣2，﹣ $\frac{1}{2}$ ，0，4中任取一个数记为m，再从余下的三个数中，任取一个数记为n，若k=mn，则正比例函数y=kx的图象经过第三、第一象限的概率是．

查看试题解析
14. 如图，将矩形纸片ABCD折叠，使边AB，CB均落在对角线BD上，得折痕BE，BF，则∠EBF=°．

查看试题解析
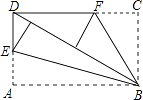15. 已知点P（a，b）在直线y= $\frac{1}{2}$ x﹣1上，点Q（﹣a，2b）在直线y=x+1上，则代数式a²﹣4b²﹣1的值为．

查看试题解析
16. 如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．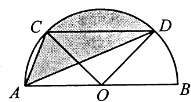

查看试题解析

三、解答题：

17. 解方程：（3x+1）²=9x+3．

查看试题解析
18. 如图，点A，B，C，D在一条直线上，△ABF≌△DCE．你能得出哪些结论？（请写出三个以上的结论）

查看试题解析
19. 2016年3月全国两会胜利召开，某数学兴趣小组就两会期间出现频率最高的热词：A脱贫攻坚．B．绿色发展．C．自主创新．D．简政放权等热词进行了抽样调查，每个同学只能从中选择一个“我最关注”的热词，如图是根据调查结果绘制的两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了名同学；

(2)、条形统计图中，m= ， n=；

(3)、扇形统计图中，热词B所在扇形的圆心角的度数是；

(4)、从该校学生中随机抽取一个最关注热词D的学生的概率是多少？

查看试题解析
20. 如图，在平面直角坐标系xOy中，双曲线y= $\frac{m}{x}$ 与直线y=﹣2x+2交于点A（﹣1，a）．

(1)、求a，m的值；

(2)、求该双曲线与直线y=﹣2x+2另一个交点B的坐标．

查看试题解析
21. 已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

(1)、求证：点D是AB的中点；

(2)、判断DE与⊙O的位置关系，并证明你的结论；

(3)、若⊙O的直径为18，cosB= $\frac{1}{3}$ ，求DE的长．

查看试题解析
22. 为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
港口
运费（元/吨）
甲库
乙库
A港
14
20
B港
10
8

(1)、设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

(2)、求出最低费用，并说明费用最低时的调配方案．

查看试题解析
23. 综合题
如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）

(1)、当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是；

(2)、当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD= $\sqrt{3}$ AD；

(3)、将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．

查看试题解析
24. 如图1，二次函数y₁=（x﹣2）（x﹣4）的图象与x轴交于A，B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．

(1)、写出点D的坐标．

(2)、点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y₂=ax²+bx+c（a≠0）的图象过点A．
①试说明二次函数y₂=ax²+bx+c（a≠0）的图象过点B；
②点R在二次函数y₁=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为时，二次函数y₂=ax²+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；
③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y₁=（x﹣2）（x﹣4）、y₂=ax²+bx+c（a≠0）的图象于点E，F，G，H（点E，G在对称轴l左侧），过点H作x轴的垂线，垂足为点N，交二次函数y₁=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．

查看试题解析

港口	运费（元/吨）
港口	甲库	乙库
A港	14	20
B港	10	8