河南省信阳九中2017年中考数学三模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. 在 ,0, ,﹣2017,0.01001这五个数中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5纳米的碳纳米管,1纳米=0.000000001米,则0.5纳米用科学记数法表示为( )A、0.5×10﹣9米 B、5×10﹣8米 C、5×10﹣9米 D、5×10﹣10米4. 在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
3. 碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5纳米的碳纳米管,1纳米=0.000000001米,则0.5纳米用科学记数法表示为( )A、0.5×10﹣9米 B、5×10﹣8米 C、5×10﹣9米 D、5×10﹣10米4. 在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )参赛者编号
1
2
3
4
5
成绩/分
96
88
86
93
86
A、96,88 B、86,88 C、88,86 D、86,865. 从1、2、3、4中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是6的倍数的概率是( )A、 B、 C、 D、6. 反比例函数y= (k≠0)图象上的两个点A(x1 , y1),B(x2 , y2),当x1<x2<0时,y1>y2 , 那么一次函数y=﹣2kx+k的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若不等式组 有解,则m的取值范围是( )A、m>2 B、m<2 C、m≥2 D、m≤28. 已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )A、k<4 B、k≤4 C、k<4且k≠3 D、k≤4且k≠39. 如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣2x+ 与⊙O的位置关系是( )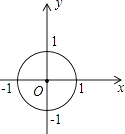 A、相离 B、相交 C、相切 D、无法确定10. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A、相离 B、相交 C、相切 D、无法确定10. 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( ) A、
A、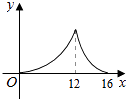 B、
B、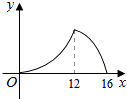 C、
C、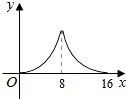 D、
D、
二、填空
-
11. 计算: +(|﹣3|)0= .12. 如图,在△ABC中,DE是中位线,若四边形EDCB的面积是30cm2 , 则△AED的面积是 .
 13. 如图,A,B是反比例函数y= 图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为 .
13. 如图,A,B是反比例函数y= 图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为 .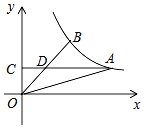 14. 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE,CF交于点G,半径BE,CD交于点H,且点C是 的中点,若扇形的半径为3,则图中阴影部分的面积等于 .
14. 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE,CF交于点G,半径BE,CD交于点H,且点C是 的中点,若扇形的半径为3,则图中阴影部分的面积等于 .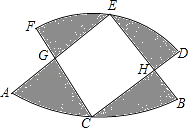 15. 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为 .
15. 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为 .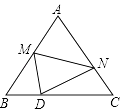
三、解答题
-
16. 先化简,再求值: ÷(a+2﹣ ),其中a为不大于3的非负整数.
17. 某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.
根据图中提供的信息,解答下列问题:
(1)、此次共调查了名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是度;(2)、请把这个条形统计图补充完整;(3)、现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目.18. 如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.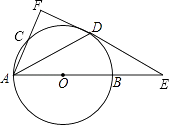 (1)、求证:AF⊥EF;(2)、填空:
(1)、求证:AF⊥EF;(2)、填空:①当BE=时,点C是AF的中点;
②当BE=时,四边形OBDC是菱形.
19. 如图,AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据: ≈1.414, ≈1.732) 20. 如图,在平面直角坐标系中,直线y=2x与反比例函数y= 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= 在第一象限内的图象交于点P,且△POA的面积为2.
20. 如图,在平面直角坐标系中,直线y=2x与反比例函数y= 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= 在第一象限内的图象交于点P,且△POA的面积为2. (1)、求k的值.
(1)、求k的值.
(2)、求平移后的直线的函数解析式.
21. 商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= ,且其日销售量y(kg)与时间t(天)的关系如表:时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)、问哪一天的销售利润最大?最大日销售利润为多少?
22. 综合题 (1)、操作发现:
(1)、操作发现:如图①,在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD=°;当∠BAP=α°(0<α<45°)时,则∠AFD=;猜想线段DF,EF,AF之间的数量关系:DF﹣EF=AF(填系数);
(2)、数学思考:如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD=;线段DF,EF,AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)、类比探究:如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD=°;请直接写出线段DF,EF,AF之间的数量关系: .
23. 如图,已知抛物线y= (x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.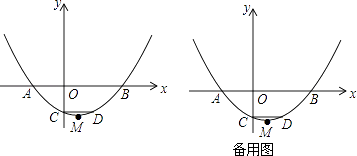 (1)、求点A,B,C的坐标;
(1)、求点A,B,C的坐标;
(2)、设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)、P是抛物线上一点,请你探究:是否存在点P,使以P,A,B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.