河北省承德市围场县2017年中考数学模拟试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数是( )A、3 B、﹣3 C、﹣ D、2. 下列命题正确的是( )A、内错角相等 B、两角及一边对应相等的两个三角形全等 C、1的立方根是±1 D、﹣1是无理数3. 下列运算正确的是( )A、 B、(﹣3a)2=3a2 C、2a+2a=4a D、a3•a2=a64. 下列等式从左到右的变形属于因式分解的是( )A、x2﹣2x+1=(x﹣1)2 B、ax﹣ay+a=a(x﹣y)+a C、x3﹣x=x(x+1)(x﹣1)+1 D、x2﹣4+3x=(x+2)(x﹣2)+3x5. 如图是由6个相同的小正方体构成的几何体,其俯视图是( )
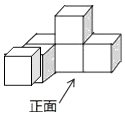 A、
A、 B、
B、 C、
C、 D、
D、 6. 九年级各班人数如图所示
6. 九年级各班人数如图所示班级
九年一班
九年二班
九年三班
九年四班
人数
36
36
42
46
则四个班的中位数和平均数分别是多少( )
A、40、39 B、36、40 C、39、39 D、39、407. 不等式组 的解集是( )A、x>﹣2 B、﹣2<x< C、x> D、无解8. 如图,直线MN是四边形AMBN的对称轴,与对角线交与点Q,点P是直线MN上面一点,下列判断错误的是( )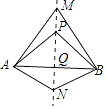 A、AQ=BQ B、AP=BP C、∠MAP=∠MBP D、∠ANM=∠NMB9. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A、AQ=BQ B、AP=BP C、∠MAP=∠MBP D、∠ANM=∠NMB9. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( ) A、6 B、8 C、10 D、1210. 对于平面图形上的任意两点P,Q,如果经过某种变换得到的新图形上的对应点P1 , Q1 , 下列变换中不一定保证PQ=P1Q1的是( )A、平移 B、旋转 C、翻折 D、位似11. 若关于x的方程x2﹣4x+c=0不存在实数根,则c的取值范围是( )A、c>4 B、c≥4 C、c≤4 D、c<412. 一直角三角形的两边长分别为6和8,则该三角形中较小锐角的正弦值为( )A、 B、 C、 或 D、 或13. 已知二次函数y=ax2+bx+c的图象如图所示.下列结论:
A、6 B、8 C、10 D、1210. 对于平面图形上的任意两点P,Q,如果经过某种变换得到的新图形上的对应点P1 , Q1 , 下列变换中不一定保证PQ=P1Q1的是( )A、平移 B、旋转 C、翻折 D、位似11. 若关于x的方程x2﹣4x+c=0不存在实数根,则c的取值范围是( )A、c>4 B、c≥4 C、c≤4 D、c<412. 一直角三角形的两边长分别为6和8,则该三角形中较小锐角的正弦值为( )A、 B、 C、 或 D、 或13. 已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④4ac<b2
其中正确的个数有( )
 A、1 B、2 C、3 D、414. 如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )
A、1 B、2 C、3 D、414. 如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )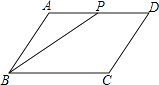 A、
A、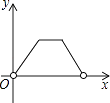 B、
B、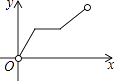 C、
C、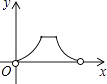 D、
D、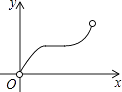 15. 如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
15. 如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )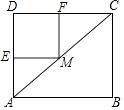 A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题
-
16. 用科学记数法表示﹣0.00000123= .17. 若a=2,b=3,则 的值为 .18. 定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1 , y1),点B坐标为(x2 , y2),把式子 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1 , y1)和B(x2 , y2),当x1=1,x2﹣x1= 时,函数K从x1到x2的平均变化率是;当x1=1,x2﹣x1= (n为正整数)时,函数K从x1到x2的平均变化率是 .
三、解答题
-
19. 已知P= (m、n≠0,m≠n)(1)、化简P;(2)、若点A(m,n)在正比例函数y=3x图象上,求P的值.20. 如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.
 21. 有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√、×、√”,B组的卡片上分别画上“√、×、×”,如图1所示.
21. 有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√、×、√”,B组的卡片上分别画上“√、×、×”,如图1所示. (1)、若将卡片无标记的一面朝上摆在桌上,再发布从两组卡片中随机各抽取一张,求两张卡片上标记都是√的概率(请用树形图法或列表法求解)(2)、若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记.
(1)、若将卡片无标记的一面朝上摆在桌上,再发布从两组卡片中随机各抽取一张,求两张卡片上标记都是√的概率(请用树形图法或列表法求解)(2)、若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记.①若随机揭开其中一个盖子,看到的标记是√的概率是多少?
②若揭开盖子,看到的卡片正面标记是√后,猜想它的反面也是√,求猜对的概率.
22. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)、写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)、求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)、若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)、若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?23. 如图,函数y= (x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.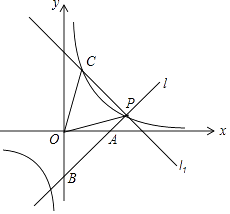 (1)、求直线l的函数解析式;
(1)、求直线l的函数解析式;
(2)、过点P作直线l的垂线l1 , 交函数y= (x>0)图象于点C,求△OPC的面积.
24. 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC.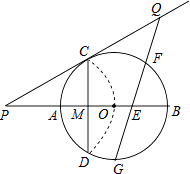 (1)、求CD的长;
(1)、求CD的长;
(2)、求证:PC是⊙O的切线;
(3)、点G为 的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交 于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.
25. 在平面直角坐标系中,正方形OABC的顶点B在第一象限,顶点A,C分别在x轴和y轴上,直线l1:x=4与直线l2:y=4相交于点E,以点E为顶点的抛物线K经过点B(6,6).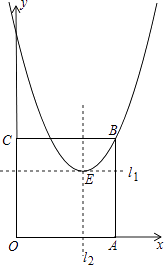 (1)、求抛物线K的解析式.
(1)、求抛物线K的解析式.
(2)、点P是线段OC上一点,点O关于AP的对称点为M,①若点M落在直线l1或l2上时,将抛物线向下或向上平移多少,使其顶点落在AM上;
②若点M落在抛物线上,请直接写出一个符合题意的点P的坐标.