甘肃省兰州三十中2017年中考数学模拟试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题:
-
1. 下面所给几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. a,b,c为常数,且(a﹣c)2>a2+c2 , 则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为03. 如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
2. a,b,c为常数,且(a﹣c)2>a2+c2 , 则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为03. 如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )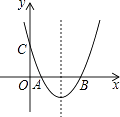 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
4. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( ) A、2:5 B、2:3 C、3:5 D、3:25. 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )
A、2:5 B、2:3 C、3:5 D、3:25. 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )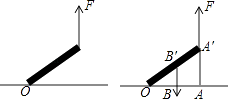 A、变大 B、变小 C、不变 D、无法判断6. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
A、变大 B、变小 C、不变 D、无法判断6. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )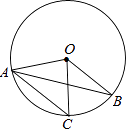 A、25° B、50° C、60° D、30°7. 一次函数y=2x﹣1与反比例函数y=﹣x﹣1的图象的交点的情况为( )A、只有一个交点 B、有两个交点 C、没有交点 D、不能确定8. 下列事件:
A、25° B、50° C、60° D、30°7. 一次函数y=2x﹣1与反比例函数y=﹣x﹣1的图象的交点的情况为( )A、只有一个交点 B、有两个交点 C、没有交点 D、不能确定8. 下列事件:①打开电视机,正在播放新闻;
②父亲的年龄比他儿子年龄大;
③下个星期天会下雨;
④向上用力抛石头,石头落地;
⑤一个实数的平方是负数.
属于确定事件的有( )个.
A、1 B、2 C、3 D、49. 如图,直线l和双曲线 交于A、B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )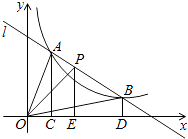 A、S1<S2<S3 B、S1>S2>S3 C、S1=S2>S3 D、S1=S2<S310. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=19611. 如图,在▱ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
A、S1<S2<S3 B、S1>S2>S3 C、S1=S2>S3 D、S1=S2<S310. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=19611. 如图,在▱ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )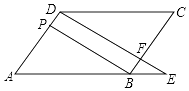 A、3 B、4 C、5 D、612. 圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )A、扩大了一倍 B、扩大了两倍 C、扩大了四倍 D、没有变化13. 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受力最大,为59.9;当提出概念30min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数关系式为( )A、y=﹣(x﹣13)2+59.9 B、y=﹣0.1x2+2.6x+31 C、y=0.1x2﹣2.6x+76.8 D、y=﹣0.1x2+2.6x+4314. 计算:cos245°+sin245°=( )A、 B、1 C、 D、15. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A、3 B、4 C、5 D、612. 圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )A、扩大了一倍 B、扩大了两倍 C、扩大了四倍 D、没有变化13. 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受力最大,为59.9;当提出概念30min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数关系式为( )A、y=﹣(x﹣13)2+59.9 B、y=﹣0.1x2+2.6x+31 C、y=0.1x2﹣2.6x+76.8 D、y=﹣0.1x2+2.6x+4314. 计算:cos245°+sin245°=( )A、 B、1 C、 D、15. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( ) A、
A、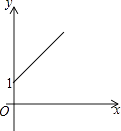 B、
B、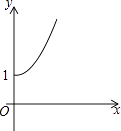 C、
C、 D、
D、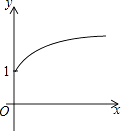
二、填空题:
-
16. 关于x的方程x2+5x﹣m=0的一个根是2,则m= .
17. 如图,正△AEF的边长与菱形ABCD的边长相等,点E、F分别在BC、CD上,则∠B的度数是 . 18. 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则△ADF的面积为 .
18. 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则△ADF的面积为 . 19. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ,则图中阴影部分面积是(结果保留π和根号)
19. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ,则图中阴影部分面积是(结果保留π和根号) 20. 如图,点P是Rt△ABC斜边AB上的任意一点(A、B两点除外),过点P作一条直线,使截得的三角形与Rt△ABC相似,这样的直线可以作条.
20. 如图,点P是Rt△ABC斜边AB上的任意一点(A、B两点除外),过点P作一条直线,使截得的三角形与Rt△ABC相似,这样的直线可以作条.
三、计算题:
-
21. 先化简,再求代数式的值.( + )÷ ,其中a=tan60°﹣sin30°.
22. 解方程:x2﹣4x+1=0四、作图题:
-
23. 已知如图,四边形ABDC坐标为A(9,0),B(5,1),C(5,4),D(2,4).

(1)、请在边长为1的小正方形组成的网格中建立平面直角坐标系,然后在平面直角坐标系中画出四边形ABDC.
(2)、求四边形ABDC的面积.五、解答题:
-
24. 我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
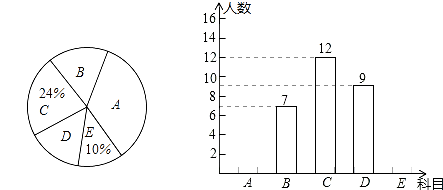 (1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人任选2人了解他们对体育选课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.25. 如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
(1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人任选2人了解他们对体育选课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.25. 如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).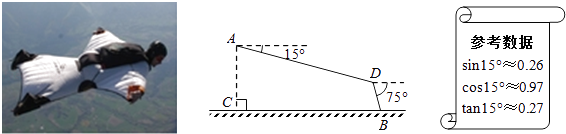 26. 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
26. 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2. (1)、若CE=1,求BC的长;(2)、求证:AM=DF+ME.27. 如图,一次函数y1=﹣x+2的图象与反比例函数y2= 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
(1)、若CE=1,求BC的长;(2)、求证:AM=DF+ME.27. 如图,一次函数y1=﹣x+2的图象与反比例函数y2= 的图象相交于A,B两点,点B的坐标为(2m,﹣m).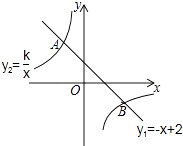 (1)、求出m值并确定反比例函数的表达式;(2)、请直接写出当x<m时,y2的取值范围.
(1)、求出m值并确定反比例函数的表达式;(2)、请直接写出当x<m时,y2的取值范围.
28. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. (1)、求∠APB的度数;(2)、当OA=3时,求AP的长.
(1)、求∠APB的度数;(2)、当OA=3时,求AP的长.六、综合题:
-
29. 已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.(1)、求抛物线的解析式;(2)、直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;(3)、连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
-