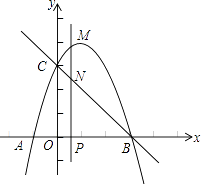甘肃省白银市平川四中2017年中考数学二模试卷
试卷更新日期:2017-11-21 类型:中考模拟
一、选择题
-
1. 下列四个图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某药品原价每盒25元,两次降价后,每盒降为16元,则平均每次降价的百分率是( )A、10% B、20% C、25% D、40%3. 反比例函数y= 的图象,当x>0时,y随x的增大而减小,则k的取值范围是( )A、k<2 B、k≤2 C、k>2 D、k≥24. 抛物线y=2(x+3)2+5的顶点坐标是( )A、(3,5) B、(﹣3,5) C、(3,﹣5) D、(﹣3,﹣5)5. 三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )A、 B、 C、 D、6. 如图所示的是一个台阶的一部分,其主视图是( )
2. 某药品原价每盒25元,两次降价后,每盒降为16元,则平均每次降价的百分率是( )A、10% B、20% C、25% D、40%3. 反比例函数y= 的图象,当x>0时,y随x的增大而减小,则k的取值范围是( )A、k<2 B、k≤2 C、k>2 D、k≥24. 抛物线y=2(x+3)2+5的顶点坐标是( )A、(3,5) B、(﹣3,5) C、(3,﹣5) D、(﹣3,﹣5)5. 三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )A、 B、 C、 D、6. 如图所示的是一个台阶的一部分,其主视图是( )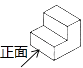 A、
A、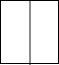 B、
B、 C、
C、 D、
D、 7. 已知k1<0<k2 , 则函数b=﹣1<0∴和y= 的图象大致是( )
7. 已知k1<0<k2 , 则函数b=﹣1<0∴和y= 的图象大致是( )
A、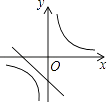 B、
B、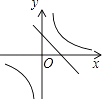 C、
C、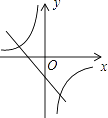 D、
D、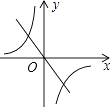 8. 在相同时刻物高与影长成比例,如果高为1.5m的测竿的影长为 2.5m,那么影长为30m的旗杆的高度是( )
8. 在相同时刻物高与影长成比例,如果高为1.5m的测竿的影长为 2.5m,那么影长为30m的旗杆的高度是( )
A、20m B、16m C、18m D、15m9. 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )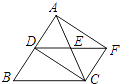 A、矩形 B、菱形 C、正方形 D、梯形10. 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )
A、矩形 B、菱形 C、正方形 D、梯形10. 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )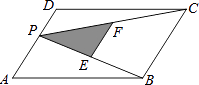 A、4 B、6 C、8 D、不能确定
A、4 B、6 C、8 D、不能确定二、填空题
-
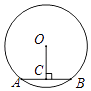
11. 因式分解:xy2﹣4x= .12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC= .
 13. 点A(2,y1),B(3,y2)是二次函数y=(x﹣1)2+3的图象上两点,则(填“>”、“<”或“=”)14. 若代数式 有意义,则x的取值范围是 .15. 已知 = ,则 .16. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
13. 点A(2,y1),B(3,y2)是二次函数y=(x﹣1)2+3的图象上两点,则(填“>”、“<”或“=”)14. 若代数式 有意义,则x的取值范围是 .15. 已知 = ,则 .16. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有 .
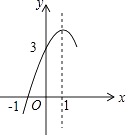 17. 如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为 .
17. 如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为 .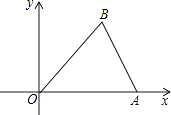 18. 观察下列等式:1=12 , 1+3=22 , 1+3+5=32 , 1+3+5+7=42 , …,则1+3+5+7+…+2015= .
18. 观察下列等式:1=12 , 1+3=22 , 1+3+5=32 , 1+3+5+7=42 , …,则1+3+5+7+…+2015= .
三、计算题
-
19. 计算:2﹣2﹣(π﹣ )0+|﹣3|﹣ cos60°.20. 先化简,再求值:( ﹣ ) ,其中x= ﹣2.21. 已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
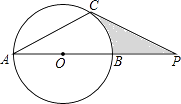 (1)、求证:CP是⊙O的切线;(2)、若PC=6,AB=4 ,求图中阴影部分的面积.22. 阅读下列材料解决问题:
(1)、求证:CP是⊙O的切线;(2)、若PC=6,AB=4 ,求图中阴影部分的面积.22. 阅读下列材料解决问题:材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)、设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).(2)、根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.(3)、根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
四、解答题
-
23. 某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
 (1)、这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
(1)、这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
24. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.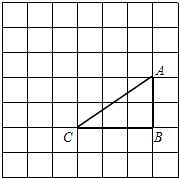
(1)、画出△A1B1C,直接写出点A1、B1的坐标;
(2)、求在旋转过程中,△ABC所扫过的面积.
25. 超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.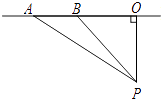 (1)、求A、B之间的路程;(2)、请判断此出租车是否超过了城南大道每小时60千米的限制速度?
(1)、求A、B之间的路程;(2)、请判断此出租车是否超过了城南大道每小时60千米的限制速度?
26. 我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)、试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)、当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
27. 如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD. (1)、求证:四边形ABEF是菱形;
(1)、求证:四边形ABEF是菱形;
(2)、若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
28. 如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.