2016年黑龙江省龙东地区中考数学试卷

试卷更新日期：2016-08-15 类型：中考真卷

进入 出卷网 下载

一、填空题

  • 1. 2015年12月6日第十届全球孔子学院大会在上海召开，截止到会前，网络孔子学院注册用户达800万人，数据800万人用科学记数法表示为人．

    查看试题解析

  • 2. 在函数y= 3x−6 中，自变量x的取值范围是 ．

    查看试题解析

  • 3. 如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件 ， 使四边形DBCE是矩形．

    查看试题解析

  • 4. 在一个不透明的袋子中装有除颜色外其他均相同的4个红球，3个白球，2个绿球，则摸出绿球的概率是 ．

    查看试题解析

  • 5. 不等式组 {x>−1x<m 有3个整数解，则m的取值范围是 ．

    查看试题解析

  • 6. 一件服装的标价为300元，打八折销售后可获利60元，则该件服装的成本价是元．

    查看试题解析

  • 7. 如图，MN是⊙O的直径，MN=4，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为 ．

    查看试题解析

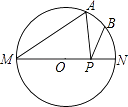  • 8. 小丽在手工制作课上，想用扇形卡纸制作一个圣诞帽，卡纸的半径为30cm，面积为300πcm2 ， 则这个圣诞帽的底面半径为cm．

    查看试题解析

  • 9. 已知：在平行四边形ABCD中，点E在直线AD上，AE= 13 AD，连接CE交BD于点F，则EF：FC的值是 ．

    查看试题解析

  • 10. 如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2016次变换后，等边△ABC的顶点C的坐标为 ．

    查看试题解析

二、选择题

  • 11. 下列运算中，计算正确的是（　　）
    A、2a•3a=6a B、（3a2）3=27a6 C、a4÷a2=2a D、（a+b）2=a2+ab+b2

    查看试题解析

  • 12. 下列图形中，既是轴对称图形又是中心对称图形的是（　　）
    A、 B、 C、 D、

    查看试题解析

  • 13. 如图，由5块完全相同的小正方体所搭成的几何体的俯视图，小正方形中的数字表示在该位置小正方体的个数，其主视图是（　　）

    A、 B、 C、 D、

    查看试题解析

  • 14. 一次招聘活动中，共有8人进入复试，他们的复试成绩（百分制）如下：70，100，90，80，70，90，90，80．对于这组数据，下列说法正确的是（　　）
    A、平均数是80 B、众数是90 C、中位数是80 D、极差是70

    查看试题解析

  • 15.

    如图，直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上，三角形沿水平线从左向右匀速穿过正方形．设穿过时间为t，正方形与三角形不重合部分的面积为s（阴影部分），则s与t的大致图象为（　　）

    A、 B、 C、 D、

    查看试题解析

  • 16. 关于x的分式方程 2x−mx+1 =3的解是正数，则字母m的取值范围是（　　）
    A、m＞3 B、m＞﹣3 C、m<3 D、m＜﹣3

    查看试题解析

  • 17. 若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为（　　）
    A、2+ 3 B、233 C、2+ 3 或2﹣ 3 D、4+2 3 或2﹣ 3

    查看试题解析

  • 18. 已知反比例函数y= 6x ，当1＜x＜3时，y的最小整数值是（　　）
    A、3 B、4 C、5 D、6

    查看试题解析

  • 19. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（　　）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 20.

    如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（　　）

    ①AE=BF；②AE⊥BF；③sin∠BQP= 45 ；④S四边形ECFG=2S△BGE ．

    A、4 B、3 C、2 D、1

    查看试题解析

三、解答题

  • 21. 先化简，再求值：（1+ 1x−2 ）÷ x2−2x+1x−2 ，其中x=4﹣tan45°．

    查看试题解析

  • 22. 如图，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）（﹣2，1），先将△ABC沿一确定方向平移得到△A1B1C1 ， 点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 ， 点A1的对应点为点A2 ．

    (1)、画出△A1B1C1；
    (2)、画出△A2B2C2；
    (3)、求出在这两次变换过程中，点A经过点A1到达A2的路径总长．

    查看试题解析

  • 23. 如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．

    (1)、求二次函数与一次函数的解析式；
    (2)、根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

    查看试题解析

  • 24. 某学校为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行八百米跑体能测试，测试结果分为A、B、C、D四个等级，请根据两幅统计图中的信息回答下列问题：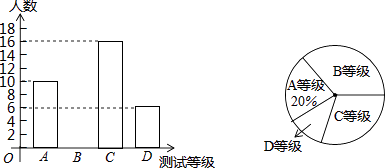

    (1)、求本次测试共调查了多少名学生？
    (2)、求本次测试结果为B等级的学生数，并补全条形统计图；
    (3)、若该中学八年级共有900名学生，请你估计八年级学生中体能测试结果为D等级的学生有多少人？

    查看试题解析

  • 25. 甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：

    (1)、A、B两城之间距离是多少千米？
    (2)、求乙车出发多长时间追上甲车？
    (3)、直接写出甲车出发多长时间，两车相距20千米．

    查看试题解析

  • 26.

    已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线BP作垂线，垂足分别为点E、F，点O为AC的中点．

    (1)、当点P与点O重合时如图1，易证OE=OF（不需证明）

    (2)、直线BP绕点B逆时针方向旋转，当∠OFE=30°时，如图2、图3的位置，猜想线段CF、AE、OE之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．

    查看试题解析

  • 27. 某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元，已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元．
    (1)、求购买一个A种品牌、一个B种品牌的足球各需多少元．
    (2)、学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案？
    (3)、请你求出学校在第二次购买活动中最多需要多少资金？

    查看试题解析

  • 28.

    如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B在x轴的正半轴上．∠OAB=90°且OA=AB，OB，OC的长分别是一元二次方程x2﹣11x+30=0的两个根（OB＞OC）．


    (1)、求点A和点B的坐标．

    (2)、点P是线段OB上的一个动点（点P不与点O，B重合），过点P的直线l与y轴平行，直线l交边OA或边AB于点Q，交边OC或边BC于点R．设点P的横坐标为t，线段QR的长度为m．已知t=4时，直线l恰好过点C．当0＜t＜3时，求m关于t的函数关系式．

    (3)、当m=3.5时，请直接写出点P的坐标．

    查看试题解析