四川省资阳市安岳县2017年中考数学模拟试卷
试卷更新日期：2017-11-09 类型：中考模拟
一、选择题
-
1. 2的相反数是（ ）A、﹣2 B、2 C、﹣ D、2. 下列计算中，正确的是（ ）A、a6÷a2=a3 B、a4•a5=a20 C、（a3）4=a12 D、a2+a2=2a43. 下列几何体中，主视图是圆的是（ ）A、
B、
C、
D、
4. 如图，直线a∥b，直线c分别与a，b相交于A，C两点，AC⊥AB于点A，AB交直线b于点B，若∠1=40°，则∠ABC的度数为（ ）
A、52° B、50° C、45° D、40°5. 在2016年龙岩市初中体育中考中，随意抽取某校5位同学一分钟跳绳的次数分别为：158，160，154，158，170，则由这组数据得到的结论错误的是（ ）A、平均数为160 B、中位数为158 C、众数为158 D、方差为20.36. 当实数x的取值使得 有意义时，函数y=4x+1中y的取值范围是（ ）A、y≥﹣7 B、y≥9 C、y＞9 D、y≤97. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连结AC，若∠A=22.5°，AB=4 ，则CD的长为（ ）
A、2 B、4 C、2 D、38. 已知抛物线y=a（x+3）2+c上有两点（x1 ， y1）和（x2 ， y2），若|x1+3|＞|x2+3|，则下列结论一定成立的是（ ）
A、y1+y2＞0 B、y1﹣y2＞0 C、a（y1﹣y2）＞0 D、a（y1+y2）＞09. 如图，在正方形ABCD中，E，F分别为AD，CD的中点，BF与CE相交于点H，直线EN交CB的延长线于点N，作CM⊥EN于点M，交BF于点G，且CM=CD，有以下结论：①BF⊥CE；②ED=EM；③tan∠ENC= ；④S四边形DEHF=4S△CHF ， 其中正确结论的个数为（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
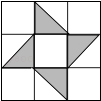
10. 计算：（﹣2）0﹣ = ．11. 小球在如图所示的地板上自由地滚动，并随机地停留在某块方砖上，那么小球最终停留在黑色区域的概率是 ．
12. 实数a在数轴上的位置如图，化简 +a= ．
13. 如图，在五边形ABCDE中，∠A+∠B+∠E=280°，DP，CP分别平分∠EDC，∠BCD，则∠P的度数是 ．
14. 如图，将矩形ABCD沿直线AC折叠，点B落在点E处，连接DE，BE，若△ABE为等边三角形，且S△CDE= ，则CD的长为 ．
15. 如图，一段抛物线：y=﹣（x﹣1）2+1（0≤x≤2）记为C1 ， 它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2 ， 交x轴于A2；将C2绕A2旋转180°得到C3 ， 交x轴于A3；如此进行下去，直至得到C8 ， 若点P（14.5，m）在抛物线C8上，则m的值为 ．
三、解答题
-
16. 先化简，再求值： ，其中 ．
17. “校园安全”受到全社会的广泛关注，我县一学校对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图所示的两幅尚不完整的统计图．（其中A表示“基本了解”；B表示“了解”；C表示“了解很少”；D表示“不了解”．）
请你根据统计图中所提供的信息解答下列问题：
(1)、请求出m的值并补全条形统计图；(2)、若该学校共有学生1200人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；(3)、已知对校园安全知识达到“了解”程度的学生中有3名女生和2名男生，若从中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．18. 为了打造成渝之心区域交通枢纽，实现安岳县跨越式发展，我县外南街直通安岳大道建设正按投资计划有序推进，因道路建设需要开挖土石方，该建设工程队计划每小时挖掘土石方540方，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，已知该公司一台甲型挖掘机与一台乙型挖掘机每小时共挖土140方，5台甲型挖掘机与3台乙型挖掘机能恰好完成每小时的挖掘量．(1)、求甲、乙两种型号的挖掘机每小时各挖土多少方？(2)、若租用一台甲型挖掘机每小时100元，租用一台乙型挖掘机每小时120元，且每小时支付的总租金不超过850元，又恰好完成每小时的挖掘量，请设计该工程队的租用方案．19. 如图，国家规定休渔期间，我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只，可疑船只正沿北偏西25°方向航行，我国渔政船立即沿北偏西70°方向前去拦截，经过1.5小时刚好在C处拦截住可疑船只，求该可疑船只航行的平均速度．（结果精确到个位，参考数据： ≈1.4， ≈1.7）
20. 如图，已知直线y=kx与双曲线y= （x＞0）相交于点A（2，m），将直线y=kx向下平移2个单位长度后与y轴交于点B，与双曲线交于点C，连结AB，AC．
(1)、求直线BC的函数表达式；(2)、求△ABC的面积．21. 如图，AB为⊙O的直径，CD切⊙O于点D，交AB的延长线于点C，CE⊥AD于点E．
(1)、求证：∠DCE=∠A；(2)、若CE=4，tan∠BDC= ，求BD的长．
22. 在平行四边形ABCD中，点E，F分别在边AD，AB上（均不与顶点重合），且∠BCD=120°，∠ECF=60°．
(1)、如图1，若AB=AD，求证：△AEC≌△BFC；(2)、如图2，若AB=2AD，过点C作CM⊥AB于点M，求证：①AC⊥BC；②AE=2FM；(3)、如图3，若AB=3AD，试探究线段CE与线段CF的数量关系．23. 如图，已知抛物线y=ax2+bx+3与x轴交于A，B两点（点A在原点左侧，点B在原点右侧），与y轴交于点C，且OB=OC=3OA，点P为线段OC上一动点，射线AP与抛物线交于点F，CD⊥AF于点E，交x轴于点D．
(1)、求此抛物线的解析式；
(2)、连结DF，若CD= ，求△BDF的面积；(3)、试判断点E能否落在此抛物线的对称轴上？若能，请求出P点的坐标；如不能，请说明理由．