陕西省2017年中考数学全真模拟试卷

试卷更新日期：2017-11-09 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{3}$ 的倒数是（）

A、 $\sqrt{3}$ B、 $\frac{1}{\sqrt{3}}$ C、﹣ $\frac{1}{\sqrt{3}}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 如图所示几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、（﹣ab）²=﹣a²b² B、（a+b）（a﹣b）=a²﹣b² C、3a²+2b=6a²b D、（a﹣b）²=a²+b²

查看试题解析
4. 把一块直尺与一块三角板如图放置，若∠2=130°，则∠1的度数为（）

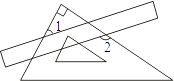A、30° B、35° C、40° D、45°

查看试题解析
5. 一次函数y=（m﹣1）x+2的图象过点（﹣2，2），m的值是（）

A、﹣1 B、1 C、2 D、3

查看试题解析
6. 如图，△ABC中，BC=8，AD是中线，将△ADC沿AD折叠至△ADC′，发现CD与折痕的夹角是60°，则点B到C′的距离是（）

A、4 B、 $4 \sqrt{2}$ C、 $4 \sqrt{3}$ D、3

查看试题解析
7. 如图，菱形OABC，OC=2，∠AOC=30°，则点B的坐标为（）

A、（ $\sqrt{3}$ ，1） B、（1， $\sqrt{3}$ ） C、（1， $\sqrt{3}$ +2） D、（ $\sqrt{3}$ +2，1）

查看试题解析
8. 已知一次函数y=kx+b的图象经过（1，a）和（a，﹣1），其中a＞1，则k，b的取值范围是（）

A、k＞0，b＞0 B、k＜0，b＞0 C、k＞0，b＜0 D、k＜0，b＜0

查看试题解析
9. 如图，已知A，B，C，D是⊙O上的点，AB⊥CD，OA=2，CD=2 $\sqrt{3}$ ，则∠D等于（）

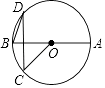A、20° B、25° C、30° D、35°

查看试题解析
10. 已知二次函数y=x²﹣2x+c的图象沿x轴平移后经过（﹣1，y₁），（5，y₂）两点若y₁＞y₂ ，则图象可能的平移方式是（）

A、向左平移5单位 B、向左平移3单位 C、向右平移1单位 D、向右平移2单位

查看试题解析

二、填空题

11. 分解因式：a³﹣9a= ．

查看试题解析
12. A．正十二边形的一个外角的度数是；
B．小明去商场乘自动扶梯由一楼去二楼，自动扶梯长约12米，已知楼层高3.4米，那么自动扶梯与地面夹角为度．（用科学计算器计算，结果精确到0.1度）

查看试题解析
13. 如图，点A在双曲线y= $\frac{2 \sqrt{3}}{x}$ （x＞0）上，点B在双曲线y= $\frac{k}{x}$ （x＞0）上（点B在点A的右侧），且AB∥x轴．若四边形OABC是菱形，且∠AOC=60°，则k= ．

查看试题解析
14. 如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．则线段EF的最小值为．

查看试题解析

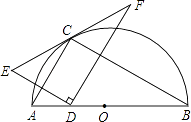
三、解答题

15. 计算：﹣3²+4sin60°﹣|1﹣ $\sqrt{3}$ |+（π﹣2017）⁰+（ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
16. 解分式方程： $\frac{4}{x^{2} - 4}$ ﹣1= $\frac{x}{2 - x}$ ．

查看试题解析
17. 如图，已知△ABC，用尺规作出△ABC外心．（保留作图痕迹，不写作法）

查看试题解析
18. 某学校欲举办“校园运动挑战赛”，为此该校在三个年级中随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查，每名学生都只选了一项．已知被调查的三个年级的学生人数均为50人，根据收集到的数据，绘制成如下统计图表（不完整）：
项目
跳绳
踢毽子
乒乓球
羽毛球
其他
人数（人）

14
10
8
6
根据统计图表中的信息，解答下列问题：

(1)、在本次随机调查中，七年级抽查班级中喜欢“跳绳”项目的学生有人，九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为；

(2)、请将条形统计图补充完整；

(3)、若该校共有3000名学生（三个年级的学生人数都相等），请估计该校喜欢“羽毛球”项目的学生总人数．

查看试题解析
19. 已知：如图，在△ABC中，D为BC上的一点，AD平分∠EDC，且∠E=∠B，DE=DC，求证：AB=AC．

查看试题解析
20. 如图，为了测量某山AB的高度，小明先在山脚下C点测得山顶A的仰角为45°，然后沿坡角为30°的斜坡走100米到达D点，在D点测得山顶A的仰角为30°，求山AB的高度．（参考数据： $\sqrt{3}$ ≈1.73）

查看试题解析
21. 某酒厂每天生产A，B两种品牌的白酒共600瓶，A，B两种品牌的白酒每瓶的成本和利润如下表：
设每天生产A种品牌白酒x瓶，每天获利y元．

(1)、请写出y关于x的函数关系式；

(2)、如果该酒厂每天至少投入成本26400元，那么每天至少获利多少元？

A
B
成本（元/瓶）
50
35
利润（元/瓶）
20
15

查看试题解析
22. 甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要通过抽签从中选出两位同学打第一场比赛．

(1)、请用树状图法或列表法，求恰好选中甲、乙两位同学的概率；

(2)、若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率．

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，点E为BC的中点，连接DE．

(1)、求证：DE是⊙O的切线；

(2)、若EC=3，BD=2 $\sqrt{6}$ ，求AC的长度．

查看试题解析
24. 如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．

(1)、求A′点的坐标；

(2)、求过C，A′，A三点的抛物线y=ax²+bx+c的解析式；

(3)、在（2）中的抛物线上是否存在点P，使以O，A，P为顶点的三角形是等腰直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

查看试题解析
25. 综合题：提出问题

(1)、问题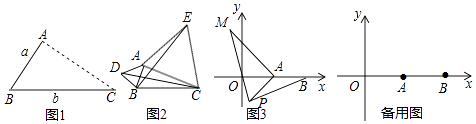

如图1，点A为线段BC外一动点，且BC=a，AB=b．
填空：当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示）

(2)、应用
点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
①请找出图中与BE相等的线段，并说明理由；
②直接写出线段BE长的最大值．

(3)、拓展：如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90，请直接写出线段AM长的最大值及此时点P的坐标．

查看试题解析

项目	跳绳	踢毽子	乒乓球	羽毛球	其他
人数（人）		14	10	8	6

	A	B
成本（元/瓶）	50	35
利润（元/瓶）	20	15