山东省济宁附中2017年中考数学二模试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. 下列四个数中,比﹣1小的数是( )A、﹣2 B、0 C、﹣ D、2. 下面四个手机应用图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 小敏的圆规摆放如图所示,则几个和小明的圆规形状一样的圆规中,与小明摆放的位似的是( )
3. 小敏的圆规摆放如图所示,则几个和小明的圆规形状一样的圆规中,与小明摆放的位似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下面是小林做的4道作业题:①2ab+3ab=5ab;②2ab﹣3ab=﹣ab;③2ab﹣3ab=6ab;④2ab÷3ab= .做对一题得2分,则他共得到( )A、2分 B、4分 C、6分 D、8分5. 某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,初四某班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是1,乙的成绩的方差是0.8.根据以上数据,下列说法正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定6. 我市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容,规定:每一位考生必须在三个物理实验(用纸签A,B,C表示)和三个化学实验(用纸签D,E,F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.小刚抽到物理实验B和化学实验F的概率是( )A、 B、 C、 D、7. 如图,双曲线y= 与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
4. 下面是小林做的4道作业题:①2ab+3ab=5ab;②2ab﹣3ab=﹣ab;③2ab﹣3ab=6ab;④2ab÷3ab= .做对一题得2分,则他共得到( )A、2分 B、4分 C、6分 D、8分5. 某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,初四某班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是1,乙的成绩的方差是0.8.根据以上数据,下列说法正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定6. 我市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容,规定:每一位考生必须在三个物理实验(用纸签A,B,C表示)和三个化学实验(用纸签D,E,F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.小刚抽到物理实验B和化学实验F的概率是( )A、 B、 C、 D、7. 如图,双曲线y= 与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( ) A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(﹣1, )8. 数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC , 小颖画的三角形面积记作S△DEF , 那么你认为( )
A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(﹣1, )8. 数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC , 小颖画的三角形面积记作S△DEF , 那么你认为( ) A、S△ABC>S△DEF B、S△ABC<S△DEF C、S△ABC=S△DEF D、不能确定9. 已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为 的是( )A、
A、S△ABC>S△DEF B、S△ABC<S△DEF C、S△ABC=S△DEF D、不能确定9. 已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为 的是( )A、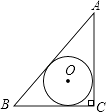 B、
B、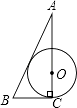 C、
C、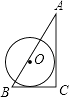 D、
D、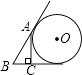
二、填空题
-
10. 计算:(﹣2)0+ ﹣ +2tan30°= .11. 把多项式m2(a﹣2)+m(2﹣a)分解因式等于 .12. 如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为 .
 13. 如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为65°,那么在大量角器上对应的度数为度(只需写出0°~90°的角度).
13. 如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为65°,那么在大量角器上对应的度数为度(只需写出0°~90°的角度).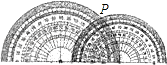 14. 如图1,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x 轴.直线y=﹣x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度y与平移的距离x的函数图象如图2所示,那么平行四边形ABCD的面积为 .
14. 如图1,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x 轴.直线y=﹣x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度y与平移的距离x的函数图象如图2所示,那么平行四边形ABCD的面积为 .
三、解答题
-
15. 先化简,再求值: ,其中a是整数,且﹣3<a<3.16. 某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号
教学方式
最喜欢的频数
频率
1
教师讲,学生听
20
0.10
2
教师提出问题,学生探索思考
3
学生自行阅读教材,独立思考
30
4
分组讨论,解决问题
0.25
 (1)、收回的问卷份数为 , 把条形统计图补充完整;(2)、扇形统计图中编号1与编号4的圆心角分别是多少度?(3)、你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.17. 如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40 厘米,∠CED=60°.
(1)、收回的问卷份数为 , 把条形统计图补充完整;(2)、扇形统计图中编号1与编号4的圆心角分别是多少度?(3)、你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.17. 如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40 厘米,∠CED=60°. (1)、求垂直支架CD的长度;(2)、求水箱半径OD的长度.18. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
(1)、求垂直支架CD的长度;(2)、求水箱半径OD的长度.18. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,乙种每件进价60元,计划购进两种服装共100件,其中甲种服装不少于65件.
(1)、若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?(2)、服装店在销售中发现:甲服装平均每天可售出20件,每件盈利40元.经市场调查发现:如果每件甲服装降价4元,那么平均每天就可多售出8件,要想平均每天销售甲服装上盈利1200元,那么每件甲服装应降价多少元?19. 问题背景在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题

下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)、“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.(2)、“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.(3)、“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度. 20. 阅读与思考;
20. 阅读与思考;婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下:
已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF
证明∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同时∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中点.
(1)、请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
 (2)、已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
(2)、已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长. 21. 如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
21. 如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD. (1)、求抛物线的函数表达式,并求出点D的坐标;(2)、如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(1)、求抛物线的函数表达式,并求出点D的坐标;(2)、如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上? (3)、在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
(3)、在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.